最近感銘を受けた日常の中の鳩の巣論法

５個の箱があります。

f:id:motcho:20160429044111p:plain

６羽の鳩がいます。

f:id:motcho:20160429044218p:plain

６羽の鳩が５個の箱に全員入ったとします。

f:id:motcho:20160429044516p:plain

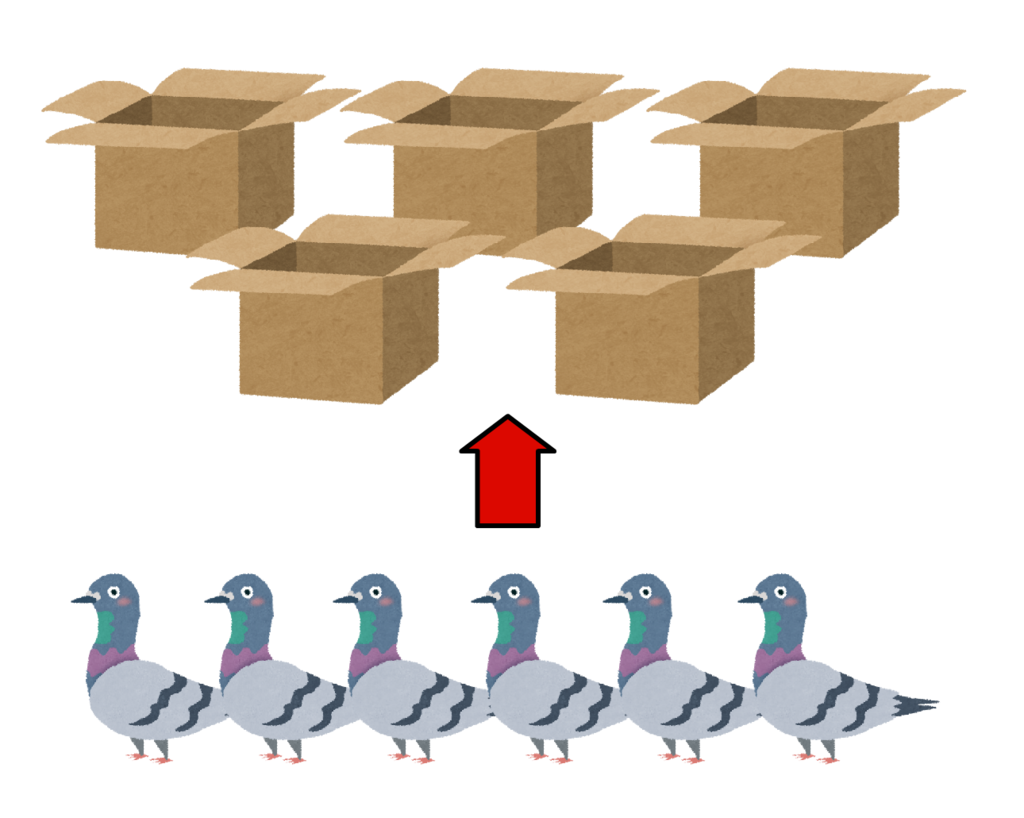
少なくとも１つの箱には、２羽以上の鳩が入っているということがわかります。

これが鳩の巣論法です。

一見自明だけど実はすごい

そう言われるとあたりまえですが、この事実を幾何学から数論からかなり広い範囲の証明問題に応用することができ、論証法としてはメジャーどころです。例えば「一辺1の正方形の内部に5つの点を打ったとき、距離が $\frac{\sqrt{2}}{2}$ 以下になる2点が必ず存在する」なんてことも証明でたりするんです。なかなか強力でしょう？　一応wikipediaも貼っときます→鳩の巣原理 - Wikipedia

この鳩の巣論法のように、「具体的なことは何もわからないが、少なくとも○○ということだけは言える」といったタイプの論法に、私はなんだかグッときてしまいます。

「具体的にどの箱にどの鳩が、みたいなことはわからないけども、少なくとも『少なくとも１つの箱には、少なくとも２羽の鳩が入っている』ということだけは確実に言える」。すごいですよね。少なくともオンパレードですもんね。わからない問題に対して、「少なくともここまでは確実に言える！」ということを少しずつ明らかにするような形でその問題に挑むなんて、有限の立場に押し込められた人類の叡智を感じます。

さておき。最近twitterとかみてて「これまさに鳩の巣論法じゃん！」と感銘を受けた事例を２つ紹介します。

「鳩の巣論法を使えばこういう問題も解ける！」的なやつではありませんのであらかじめご了承ください。たぶんそういうのは他所のブログとかにいっぱいあります。

エレベーター

まずはこちら。

エレベーターで乗ってる人の数と押されてるボタンの数で「どこかの階で必ず二人以上降りるな…」なんてぼんやり考えることあるんだけど、あれ鳩ノ巣原理って言うのか…初めて知った。
ピクロスの塗り確定マスの決定手法に通じるものがあるな。
— さわちゃそ (@sawachaso) 2016年1月20日

うおおおおお！確かに！！！

そんなこと思いもよりませんでした。自分で気づきたかった感がありちょっと悔しいです。もし自分がエレベーター乗ってて「あっこれどこかの階で必ず二人以上降り…これ鳩の巣論法やん！！！」って気づけたら興奮するでしょうね。このツイート見て以降、エレベーター乗るたびにソワソワするようになったことは言うまでもありません。

なんでや！

もう一つはこちら。

@donnay1224
どね
記録 03:34:00.005 (トップ+00.005)
順位 6位/1091人
使用クライアント Twitter Web Client
— 334Ranker (@334Ranker) 2016年3月20日

ええと、まあその、twitterにはですね、深夜3時34分ピッタリに「334」ってツイートしたやつが強い、みたいな文化があってですね、0コンマ何秒を争う熱い戦いが日夜繰り広げられていましてですね、そんでどねさんっていうのは私のフォロワーの方なんですが、まぁこの日はその方が「334」ってツイートした時間が03:34:00.005だったというわけです。それで6位だったと。

はい！　ほら！　鳩の巣論法ですよね！　わかりますか！

つまり、この競技(?)では3:34より先にツイートした人は認められないので、6位で+00.005ということは0.005秒の間に6人がひしめいていることになるわけです。0.001秒を箱、人を鳩だと考えて、「（少なくともどこか1つの0.001秒間では）2人以上が同着だった」といえるわけなんですよ！　ね！　鳩の巣論法でしょう！

※追記：+0.000秒が1位なんだから+0.005で6位なんだったら0.000、0.001、0.002、0.003、0.004、0.005って６人でぴったり収まるじゃんってご指摘を受けました。そのとおりですね。0.000秒のことを忘れていました。でもそれだとこの話成り立たなくなっちゃうから「6位が+0.004秒だった」みたいなことに脳内補完してください！「この事実に鳩の巣論法を見出すことができるよ」っていうこと自体は間違ってないですから！すいません！