今日は楽しいパーティです。
白雪姫は、円形のケーキを作りました。
白雪姫
円形のケーキに上から１回だけ包丁を入れると、最大２分割できます。
２回包丁を入れると、最大４分割までできます。
では、３回包丁を入れると最大で何分割できるでしょうか。そのまま考えると、６分割でしょうか？
上図のように切れば、最大で７つに分割することができます。
ちなみに回包丁を入れると最大
分割、
回だと
、
回だと
、そして
回だと最大
個のピースに分割できることがわかっています。なるべく多く線が重なるように切ればいいのです。実際にやって確かめてみたい感じありますが、しかし今回の本題はそこではないのでまたこんどにしましょう。
白雪姫は、王子様からもらった大切な包丁をあまり使いたくなかったので、ケーキに３回だけ包丁を入れて７つに分割し、それを７人のこびとたちに下図のように配ることにしました。
こびとたち
しかし、このような切り方では大きさがバラバラになってしまいます。包丁はあまり使いたくなかったくせにできるだけ公平に配ってあげたかった白雪姫は、そこで考えました。
「円形のケーキに３回（対称に）上から包丁を入れて７分割するとき、できるだけピースの大きさのばらつき具合を小さくするには、どう切ればよいか？」
ピースの大きさをできるだけ公平にするには、「ばらつき具合」を小さくすればいいだろう、というわけです。これが今回の問題です。
あ、一応ケーキは円柱であり、上面の面積がそのままピースごとの大きさになるということにしておきましょう。
「どう切れば」とは？
「円形のケーキに３回、対称に包丁を入れて７分割する」といっても、上図のようにケーキの中心からの距離によって、さまざまな切り方がありえます。どのように切っても７つのピースをまったく同じ大きさにすることはできませんが、できるだけ「ばらつき具合」を小さくできるのはどこかな？ということなら考えることができます。
「ばらつき具合」とは
「ばらつき具合」は、統計学の言葉で「分散」といい、ちゃんと数学的に定義されています。例として、次のような２組のトリオを考えてみます。
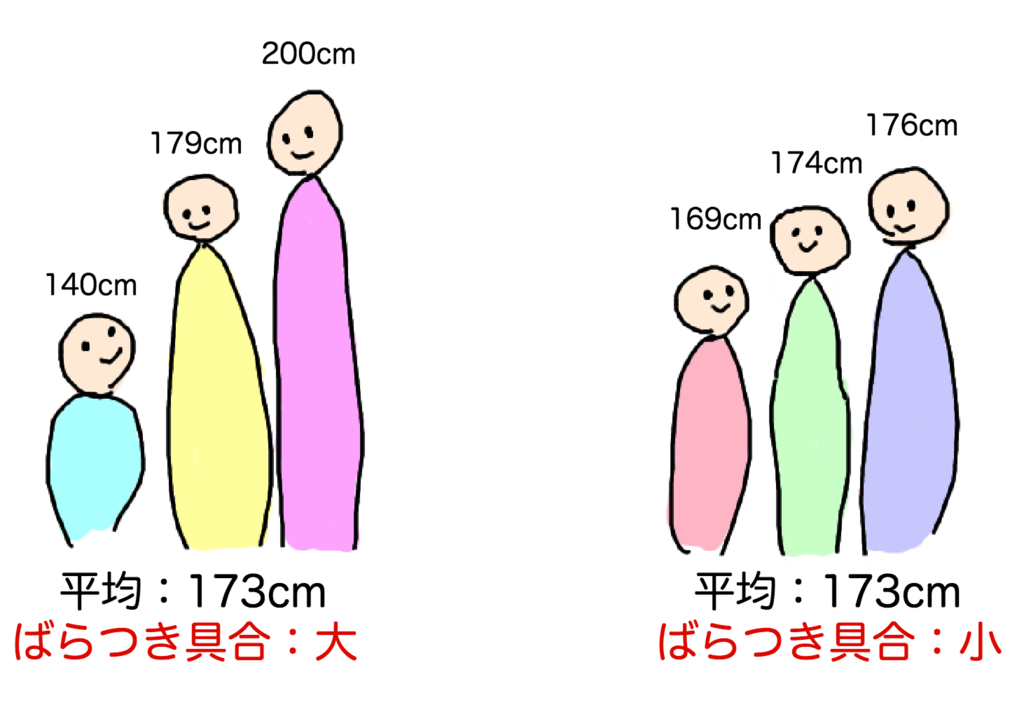
２組のトリオは、平均身長は同じですが、身長のばらつき方は違います。左側のトリオの身長は右側のトリオに比べバラバラ、すなわち「ばらついて」います（分散大）。対して、右側のトリオの身長は左側のトリオに比べ「まとまって」いるといえます（分散小）。
この図さえ見れば直感的に「分散」というものが捉えられそうですが、もちろん直感だけで定義されているわけではありません。
個の値
があり（上の例で言うとそれぞれの身長のことです）、その平均を
とします。このとき、値
の分散は、次の式で表されます。
どうなっているかわかるでしょうか。式の形をよく見ると「個の値を足して、それを
で割っている」という形をしていることがわかります。この形、なんだか見覚えありませんか？ そう。「平均」と同じ形なんですね。「
個の値を足して
で割るもの」といえば平均です。すなわち分散とは、「何かの平均」であるわけです。
ではその何かとは何なのか。式で言うとの部分のことです。これはつまり、「それぞれの値の平均との差」を表しています。
さっきの身長の話で言うと、左側のトリオにおいて、cmの人の平均との差は
で
です。
cmの人だと
で
になります。
cmの人だと
となります。この３つの値のさらに平均を取れば、「ばらつき具合」、すなわち「分散」が定量的にわかるだろう、というわけです。
2乗がついている意味もここにあります。それぞれの値が平均とどれだけ離れているか「だけ」を見たい、すなわち、値が平均より上か下かは気にしないので、2乗することで符号を揃えているのです（だったら絶対値使えばいいじゃんと思うかもしれませんが、絶対値を使うタイプの分散もあります。分散は状況や目的によっていろいろな種類があります。今回2乗を使っているのはそのほうが絶対値より計算が楽だからです）。
ここで実際に、２組のトリオそれぞれの身長の分散を求めてみましょう。２組とも平均はcmです。
左のトリオ：
右のトリオ：
おお。と約
。自分で例を挙げといてなんですが、ここまで大きな差になるとは思いませんでした。しかしこれで、「値がばらついているほど分散が大きくなる」ということはご理解いただけたかと思います。
「平均との差のさらに平均を取る」だなんて、実に「ばらつき」というものをうまくとらえていて感心します。このように、現実の概念を定式化、定量化するにはどうするのが妥当か考えることも、数学の楽しみのひとつであるといえるのではないでしょうか。
（実はこのへんの話、最近では高校数学でしっかり教えられているようなのです。時代は変わりましたね。）
ケーキの話
本題に戻ります。ではどこで切れば、ピースの大きさの分散を最も小さく抑えられるでしょうか。
説明の便宜のため、形に名前をつけておきます。
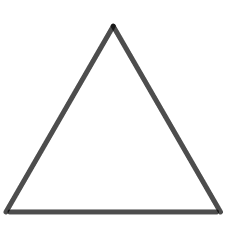を、「正三角形」
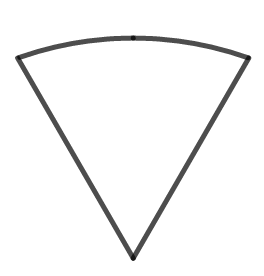を、「ピザ型」
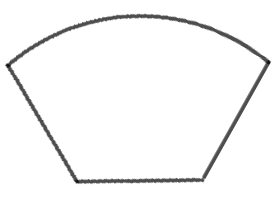を、「くし型」と呼ぶことにします。
いくつかの切り方で、ためしに分散を計算してみましょう。
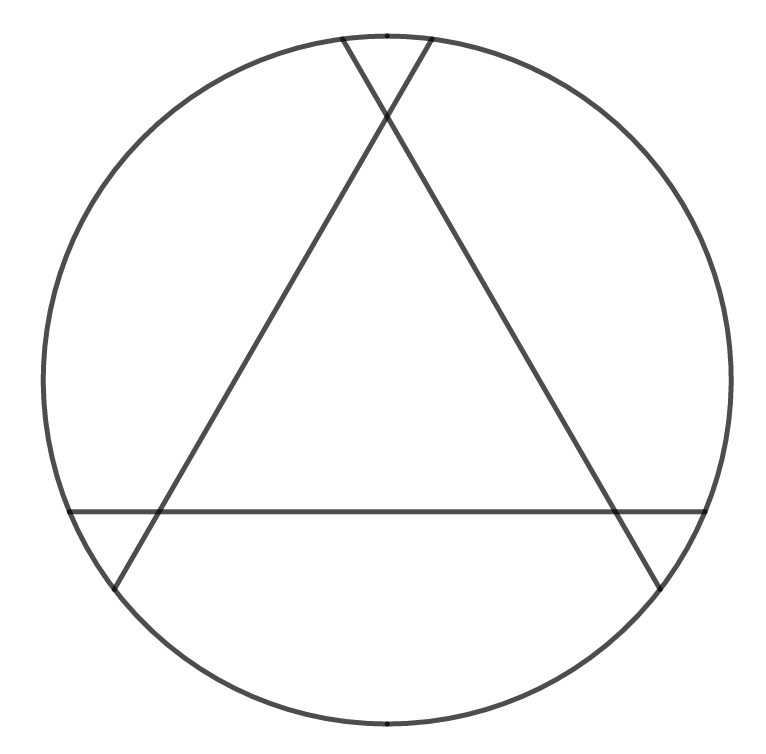
↑このあたりで切るとどうでしょうか。これはちょうど正三角形とくし型が同じ面積になるポイントです。
ここで切った場合、ケーキの半径をとすると、
正三角形の面積：
ピザ型（ひとつ分）の面積：
くし型（ひとつ分）の面積：
分散：
これだけでは比べられないのでもう少しやってみます。
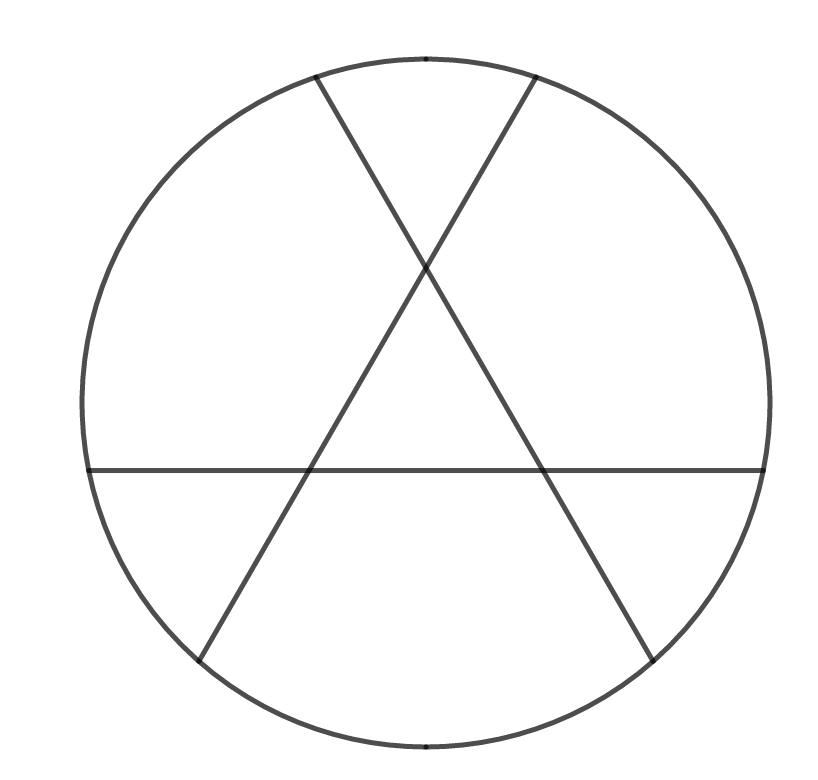
↑このあたりではどうでしょうか。こんどは正三角形とピザ型が同じ面積となっています。なんとなく、こちらのほうが分散が小さい、つまりより公平に分けられそうに見えます。
正三角形：
ピザ型：
くし型：
分散：
予想通り、こちらのほうが分散は小さくなっていました。これより分散の小さい切り方はあるでしょうか。包丁を入れる位置と分散との関係をグラフにしてみました。
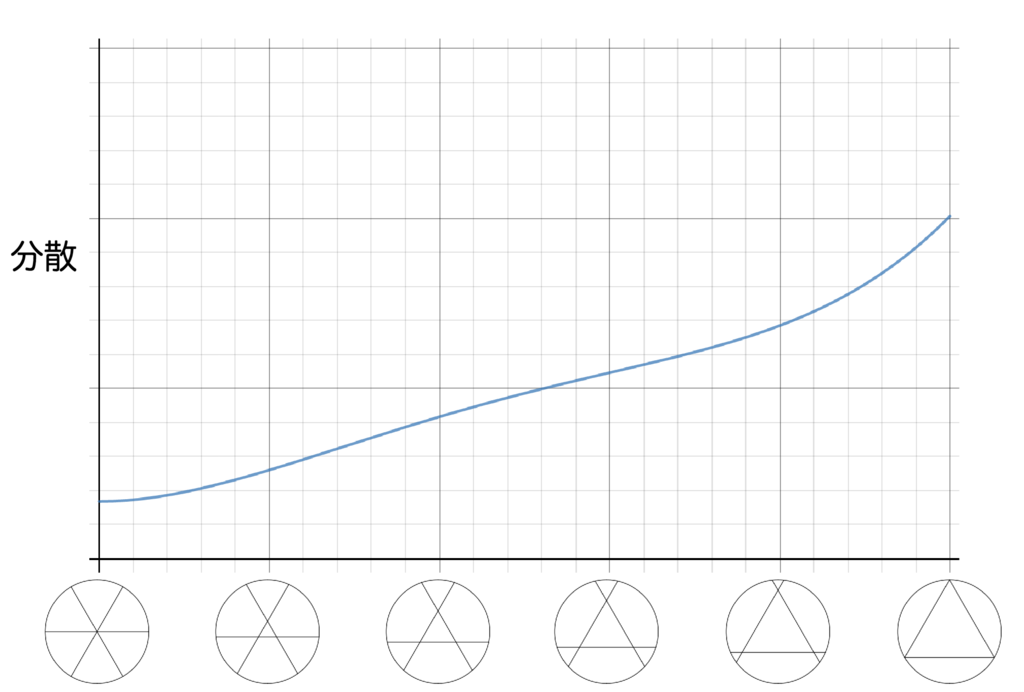
あっ。
なるほど。
包丁を入れる位置が中心に近づけば近づくほど、分散の値は小さくなっています。一番小さいところはです。
というわけで答えが出ました。
円形のケーキに３回（対称に）上から包丁を入れて７分割するとき、できるだけピースの大きさの分散を小さくするには、
↑このように切ればいいことがわかりました。つまり、中心の正三角形一つを犠牲にしてほかの６つの大きさを揃えたほうが、全体としての分散は小さくなる、ということになります。
...。
というわけで
今日は楽しいパーティです。
白雪姫は、円形のケーキに対称に３回だけ包丁を入れて、最もばらつきが小さくなるように分割しました。そしてそれぞれのピースをこびとたちに配りました。
緑のこびと「しらゆきひめ！ありがとう！」
紫のこびと「とってもおいしいケーキだなあ！」
楽しいパーティはいつまでも、いつまでも続きましたとさ。
めでたしめでたし。
