816と663の最大公約数は51です(挨拶)。
みなさんは今日も最大公約数を求めていますか? そうですか〜
いくつか整数があったときに、それらを「共通して割り切る数」が「公約数」であり、その中で最大のものが最大公約数です。
例えば42と30だったら最大公約数は6ですね。当然これらは1でも2でも3でも両方割り切れるけれども、その中で最大のものをとると6だよ、ってことです。
さて、そんな最大公約数に関しては、以下のような興味深いビジュアル表現が知られています。

なるほど〜。いい図ですね。
横に42、縦に30であるような長方形を用意して、その長方形の各辺を同時にピッタリ埋め尽くすような最大の正方形を考えると、その一辺の長さは6である、ということを表現しているんですね。
これが例えば一辺7や5の正方形で埋め尽くそうとすると、ハミ出たり足りなかったりします。一辺2や3でも埋め尽くすことはできますが「最大」ではありません。
「ピッタリ埋め尽くす」というのがまさに「割り切る」ことのうまい対応になっていて、だからこそこれで最大公約数が表現できているということなのです。
冒頭で挙げた816と663みたいな例でも、以下のように表現できます。
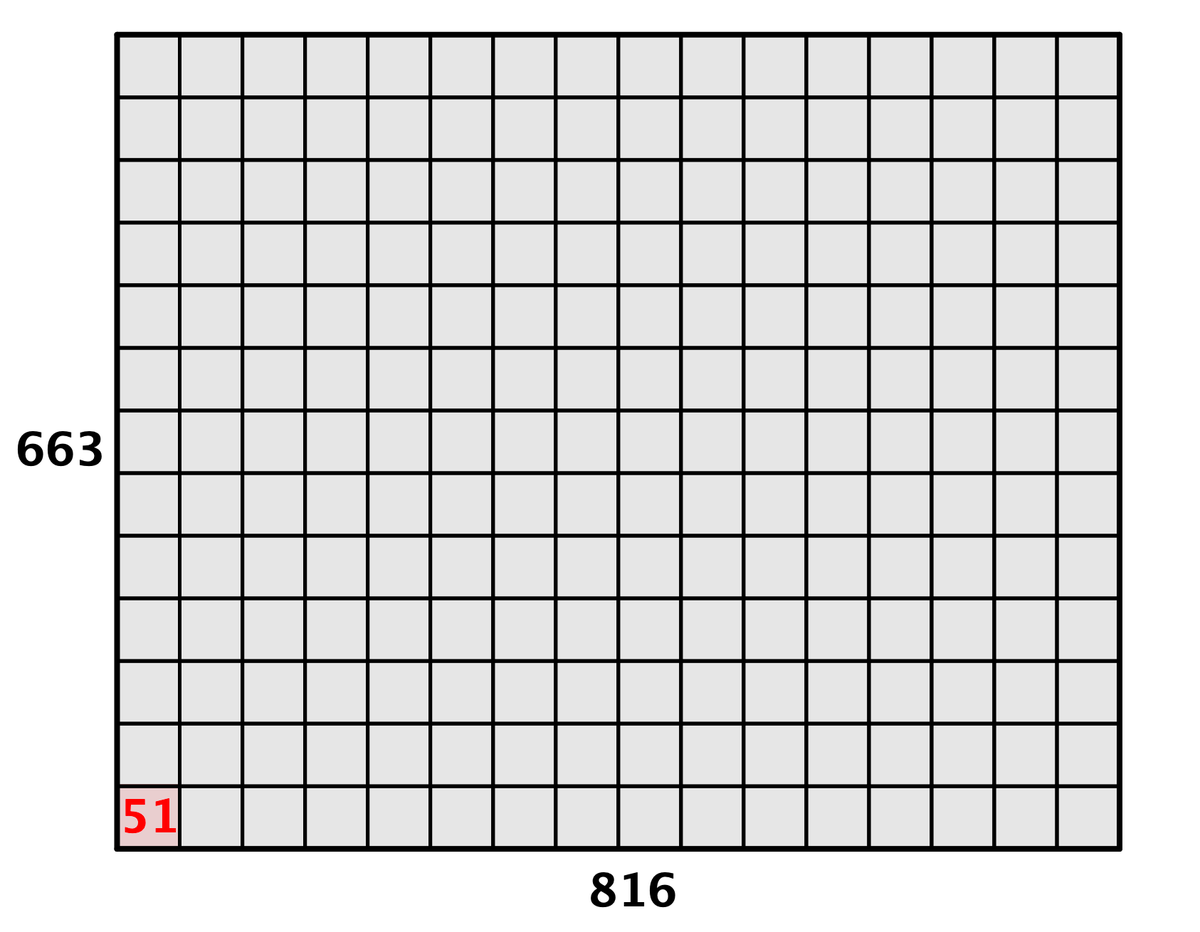
よくできてるな〜
実際に最大公約数を求めたい
さて、ということは、です。
2つの数があって、それらの最大公約数が何なのかを「実際に求めたい」とします。そんなときはこの正方形を見つける方法さえ分かればよい、ということになります。見つかった正方形の一辺の長さが分かればいいわけですから。
これが42と30みたいな例だったら、両方簡単に素因数分解ができるおかげですぐに6だとわかるのでいいですが、それこそ816と663みたいな例だと素因数分解するのは少し大変です。ましてや「767303と342516」みたいに言われるとちょっと手も足も出ません。
そんなときこそ、この「正方形を見つける」方法が効力を発揮するんですね。
ここからは実際にそのやり方を見てましょう。一般に、ある2つの数aとbで長方形を作ったとき、それをピッタリ埋め尽くす正方形を見つけたいときには、次のような方法が使えます。
正方形を見つける方法
816と663の例でやりましょう。まずはこの長方形から、
切り取れるだけ正方形を切り取ります。
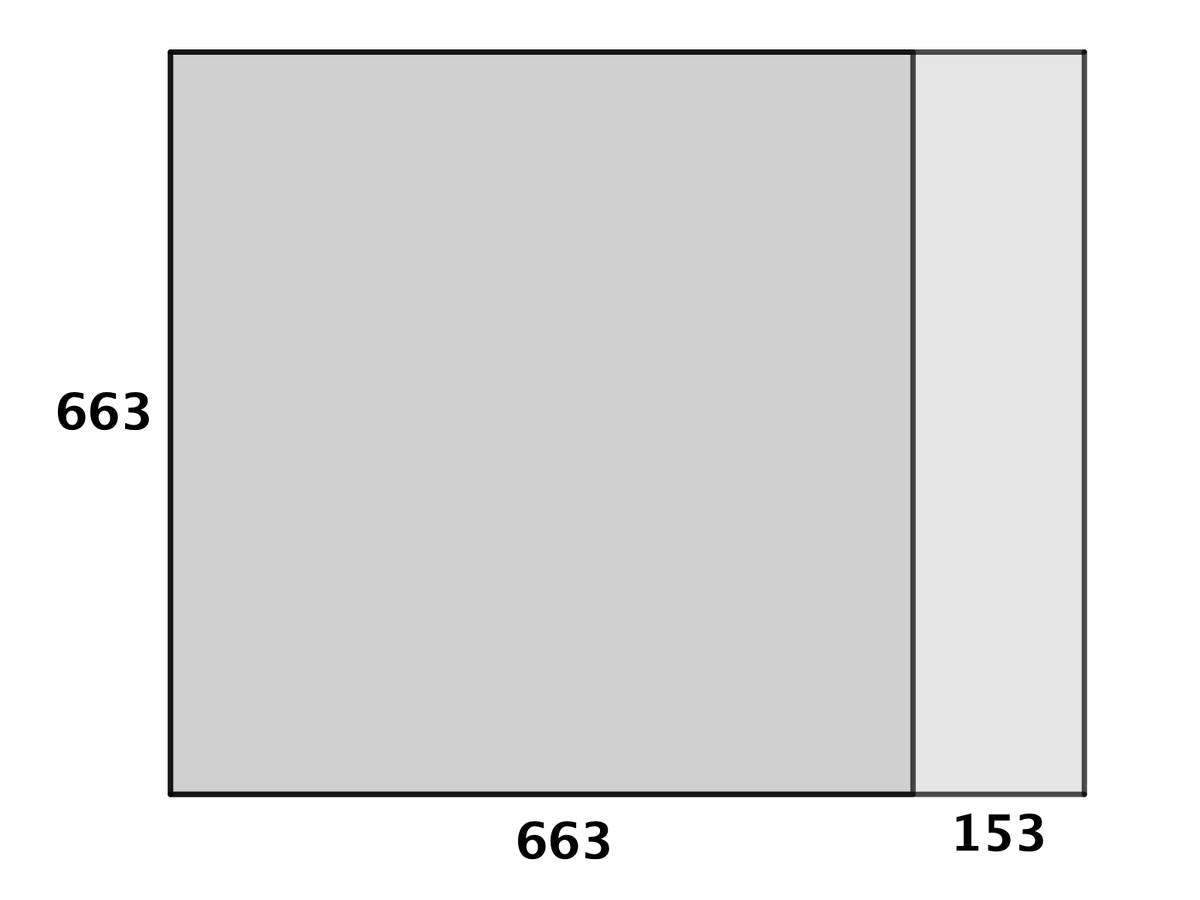
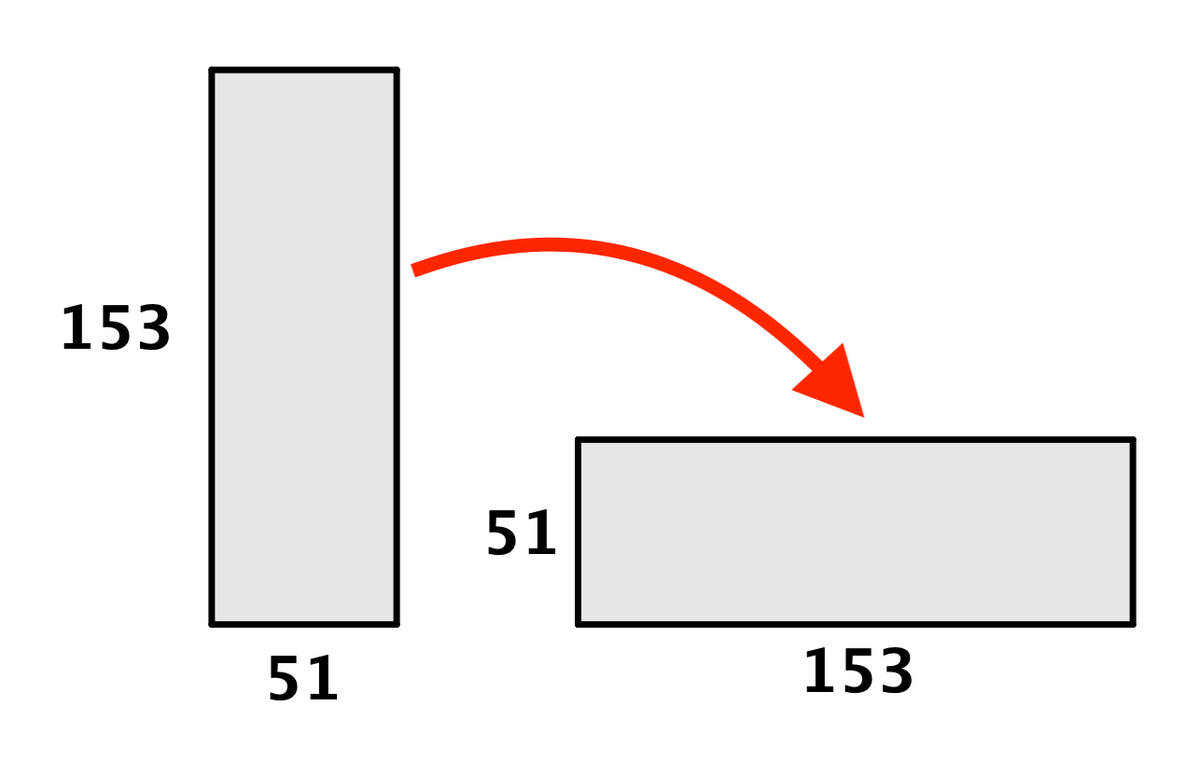
そして残ったこの長方形からも(見え方を統一するため、横に倒します)、
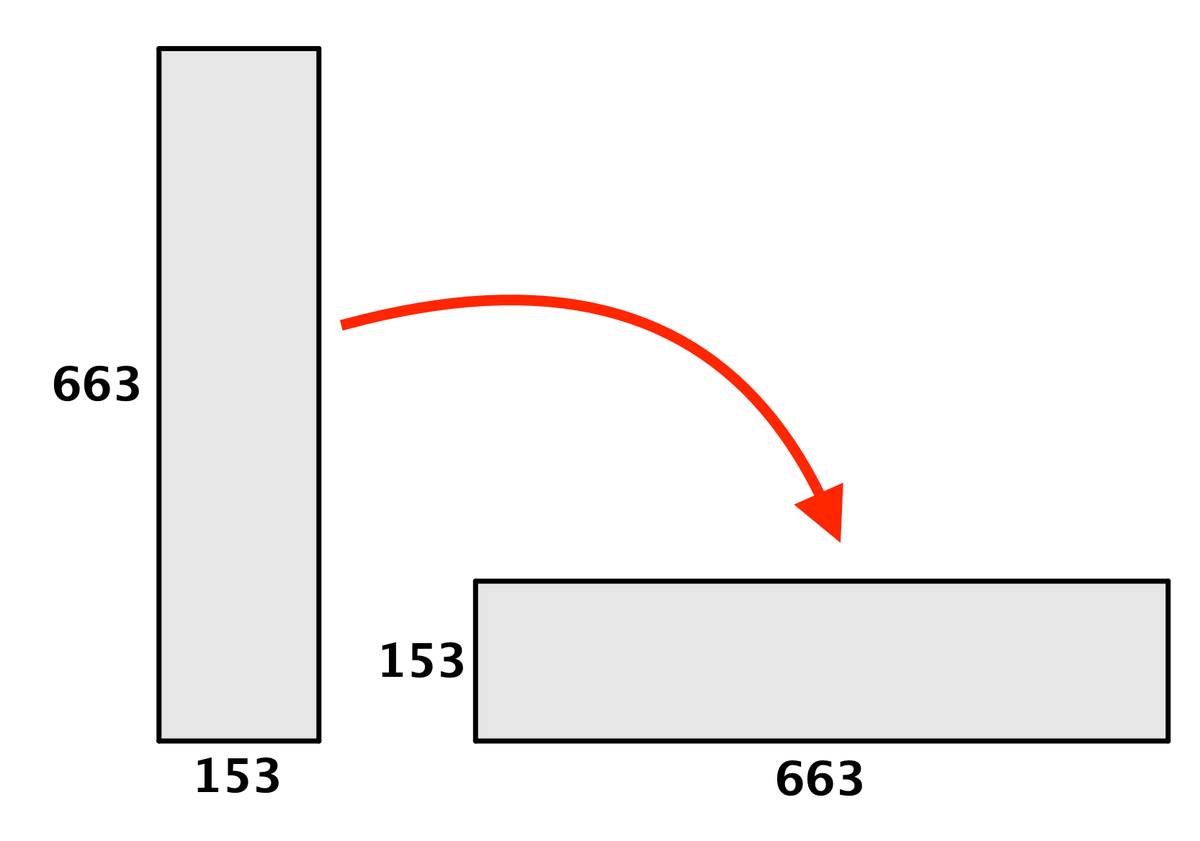
切り取れるだけ正方形を切り取ります。
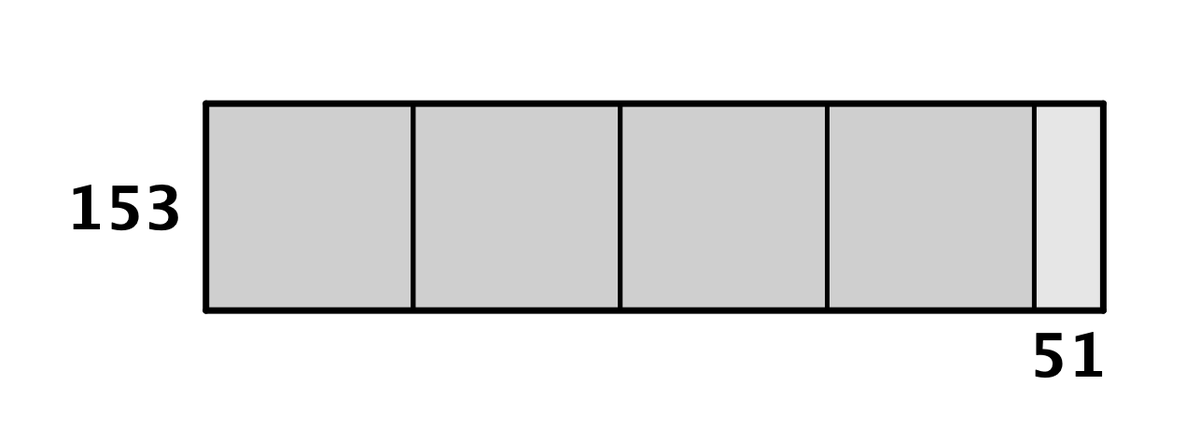
4つも切り取れました。やったね。以降、この操作を繰り返すと、
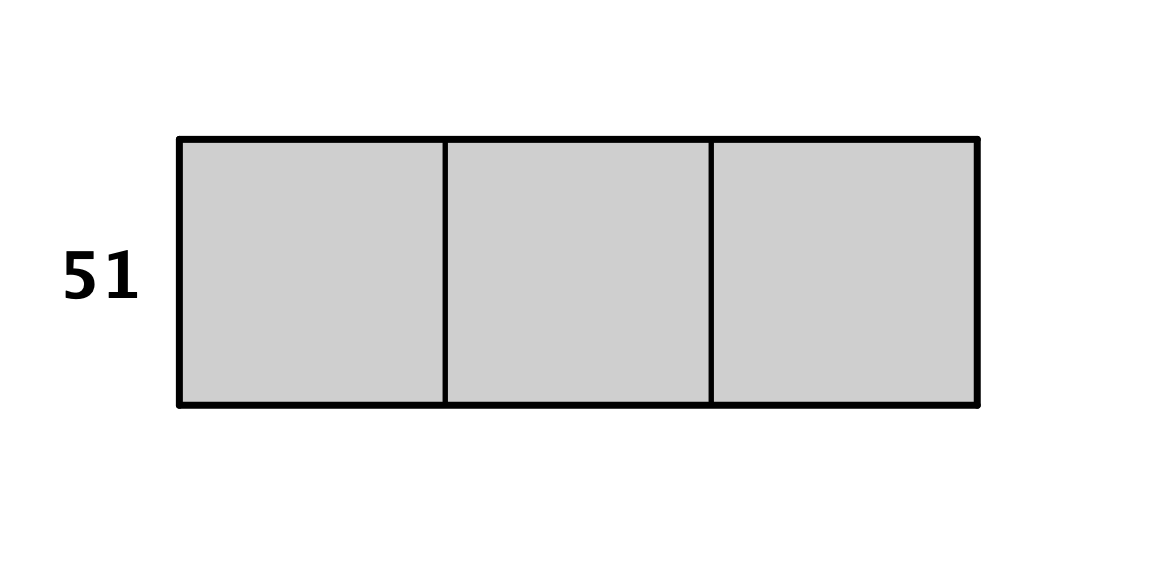
最終的に正方形でピッタリ切り取りきって終わります。
この「切り取りきった」ときの正方形の一辺の長さこそが、縦横2つの数の最大公約数である、というわけです。確かに最後に残った51というのは816と663の最大公約数になっていますね(816 = 16 × 51、663 = 13 × 51)。
この一連を一枚にまとめてみるとこういうことになってます。
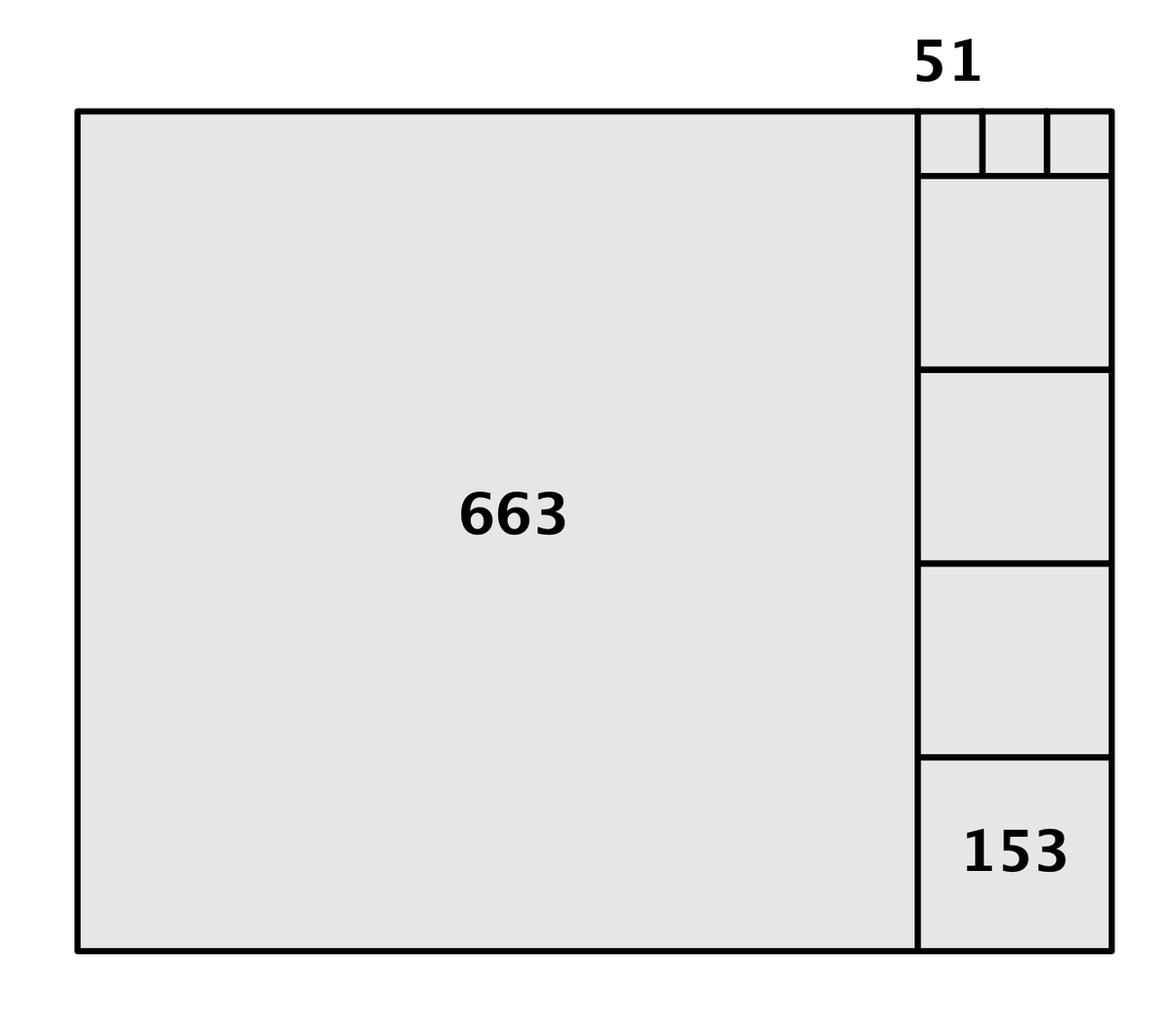
スッキリピッタリ気持ちいいって感じです。
別の例でも見てみましょう。上で出てきた「767303と342516」の場合です。
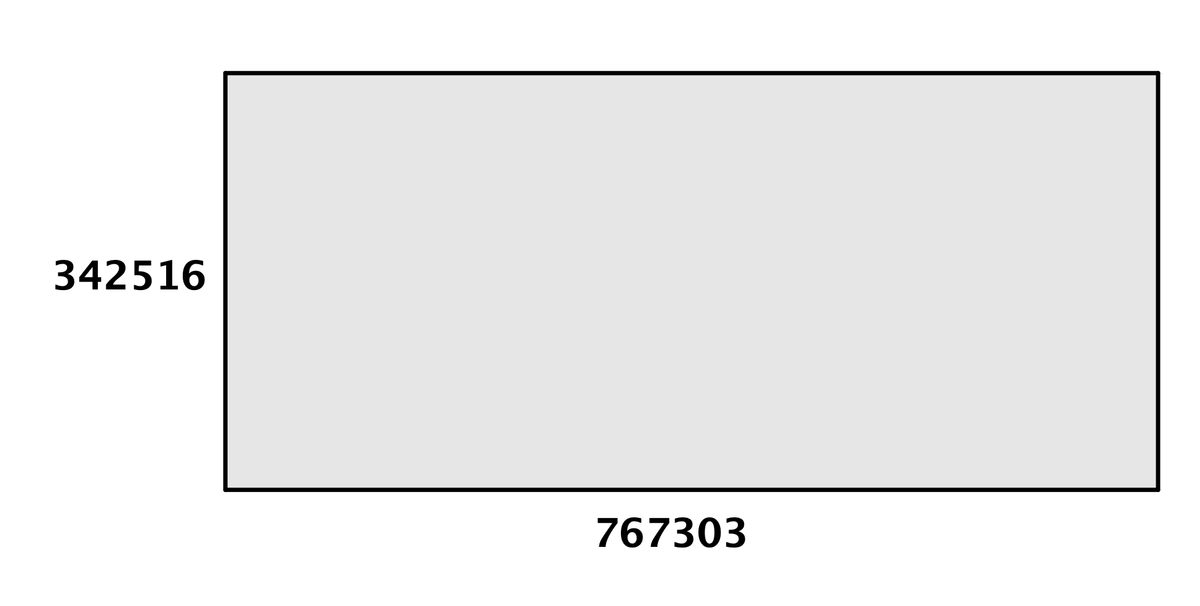
767303と342516の長方形からは、まず2つ正方形が切り取れます。
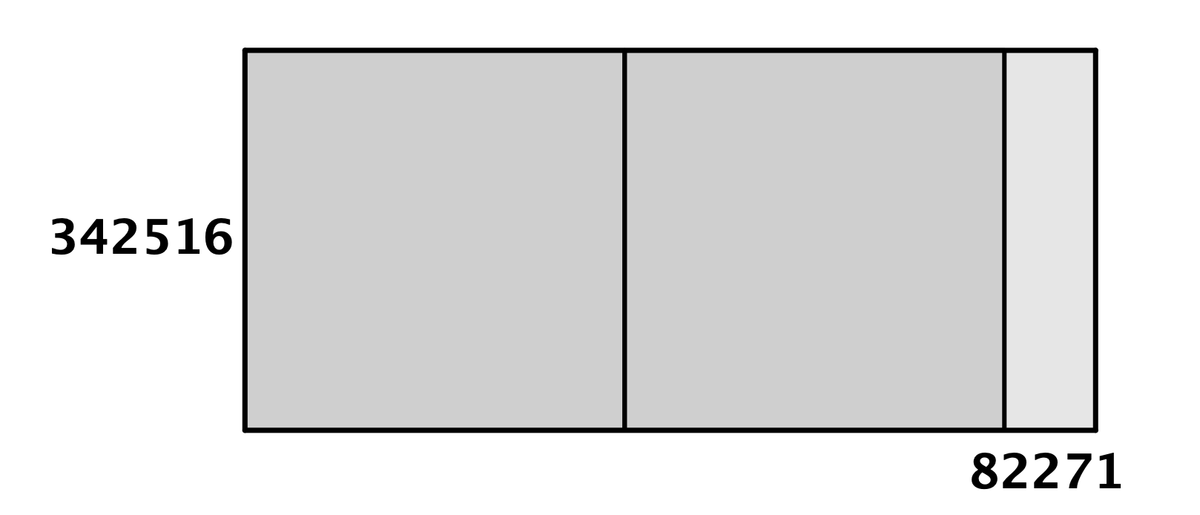
そして右端に残った長方形を横倒しにすると、こいつからは4つまで切り取れます。
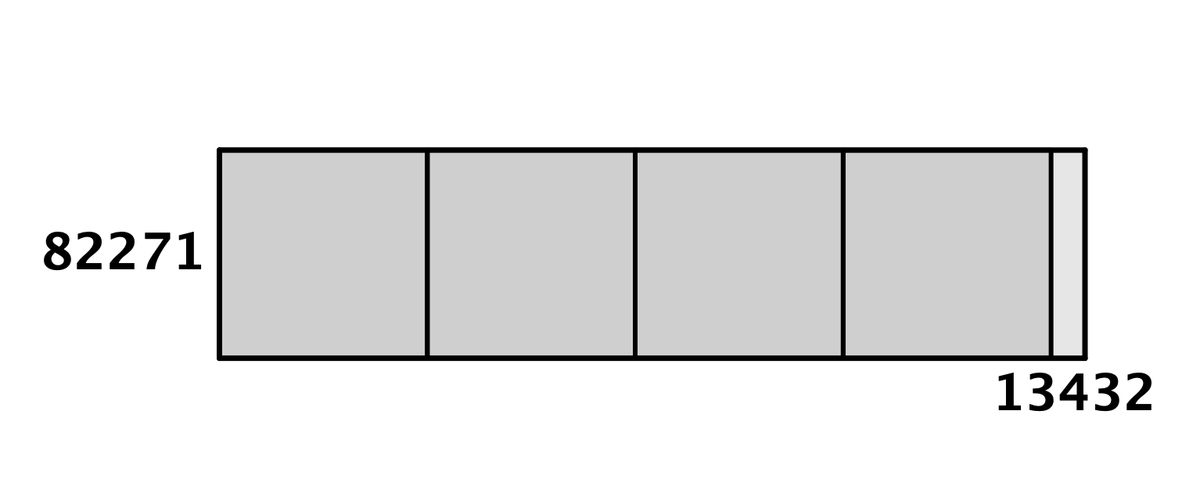
次は6つ。
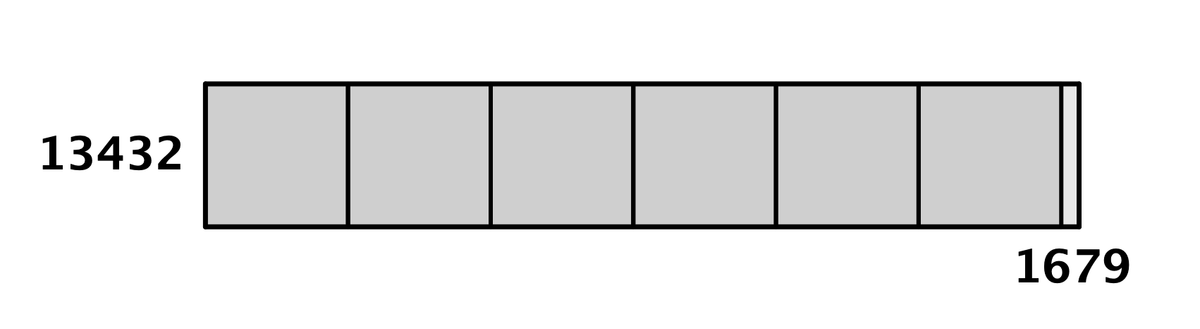
そして、8つ。
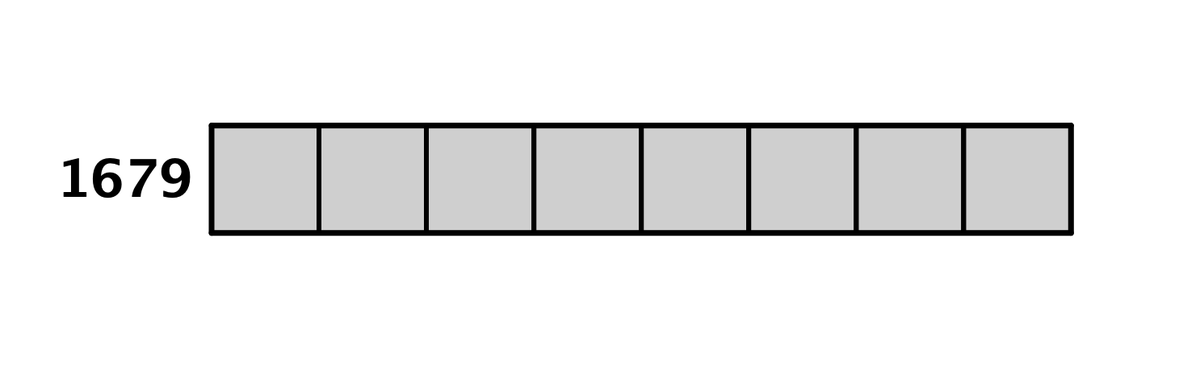
最終的に8つの正方形でピッタリ切り取りきることができて、その正方形の一辺の長さは1679だったので、767303と342516の最大公約数は1679だとわかりました(767303 = 457 × 1679、342516 = 204 × 1679)。
この一連の手続きのことを「ユークリッドの互除法」といいます。この方法は最大公約数の見つけ方としては、2つの数をそれぞれ素因数分解してやる方法よりも圧倒的に楽(計算量が少ない)であることが知られています。
ユークリッドの互除法
これまでは「長方形」になぞらえてユークリッドの互除法を見てきたわけですが、じゃあそれって実際のところどんな計算をしていることになるのか?という部分の話をしましょう。
ユークリッドの互除法の最初の操作であった「長方形から正方形を切り取れるだけ切り取る」という操作は、「長辺の長さを短辺の長さで割ったあまりを求める」ことに相当します。どういうことか。
数学と縁遠い人だと普段あまり意識に上ることは少ないかもしれませんが、割り算の「商」というのは「(割られる数から割る数を)引けるだけ引いたときの、引いた回数」のことです。マイナスにならない範囲で。
他方、「引けるだけ引いたときの、残り」が「あまり」です。
例えば50÷6は8あまり2ですが、それは「50から6を引けるだけ引くと、8回引けて、2あまる」ということだと捉えられる、って話です。
「引き算の繰り返しが割り算である」と見ることもできるでしょう。このあたりは足し算の繰り返しがかけ算であることと対応していますね。
そういうわけで、「長方形から正方形を切り取れるだけ切り取る」をすると、切り取られた結果として「長辺の長さを短辺の長さで割ったあまりの長さを持つ辺」が出てくるということだったのです。
文章だとちょっと煩雑ですね、こういうことです。
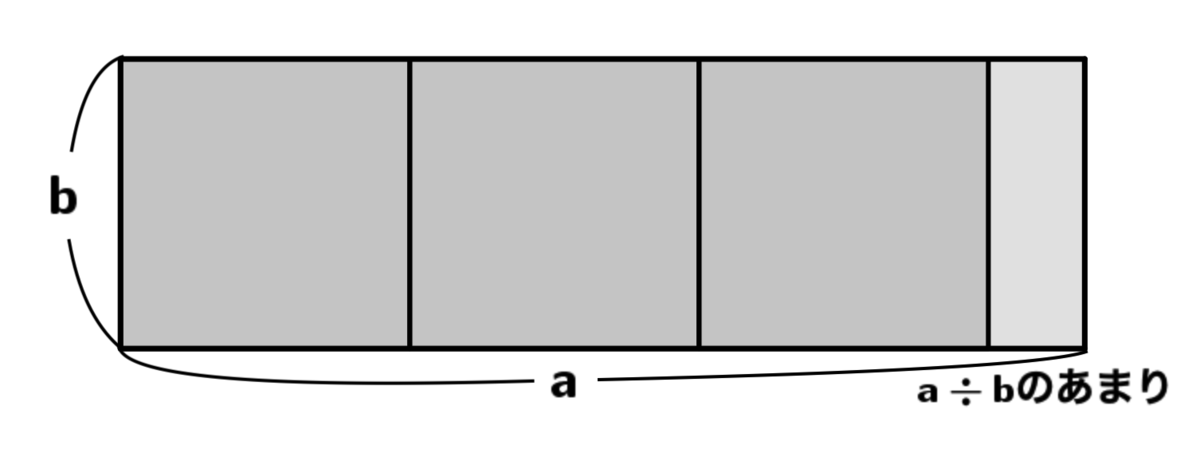
図で見るとそりゃそうだろ感が出ますね。
そして次の操作ですが、残った縦長の長方形をパタンと倒して、また同じ操作を繰り返していますね。
これはそのまんまです。すなわち、最初の長方形で行ったのと同じことを、次に出てきた長方形でもまたやるということ。
数学的な言い方に直すとこうです。最初の操作とは2数「a」と「b」について(a≧bとします)、大きい方「a」を小さい方「b」で割って、そのあまりを求めることでした。このあまりを仮に「c」としましょう。
そして次の操作とは、それと同じことを「b」と「c」を使って行う、ということに相当します。すなわち「bをcで割って、そのあまりを求める」ということ。このあまりを今度は「d」とおきましょう。
そうすると今度は「c」と「d」で作られてるような長方形が出てきて、cをdで割ったあまりを求めることができるようになって……。以下繰り返し。
なんのことはない、正方形でスッと切って長方形をパタンと倒す操作を繰り返していくことを数学的に表現したに過ぎません。
これが文章で書くとなんか煩雑に見えるのは、逆に言えばそれだけあの「長方形」の方法が優れたビジュアライズであることを示していると言えるかもしれませんね。
最後の正方形が最大公約数になっている理由
ひとつ大事なこととして、そもそもこの方法で求められた正方形の一辺が本当にちゃんと2数の最大公約数になっているのか、というのはそんなに明らかなことではありません。
実はこのことは、「aとbの最大公約数は、bとc(=aをbで割ったあまり)の最大公約数と等しい」という定理に支えられています。
長方形の話で言い換えるなら、「最初の長方形の2辺の最大公約数は、2番目の長方形の2辺の最大公約数と等しい」という言い方になるでしょう。
てことは、3番目、4番目、それ以降の長方形についても、2辺の最大公約数は等しいまま変わらない、ということになりますね。
そうやって最大公約数を保ったまま長方形をどんどん小さくしていって、最終的に縦が横を割り切って最大公約数が判明したなら、ひるがえって、それはもとの長方形においても最大公約数になっているんだよ、なぜならこの操作によって最大公約数は保たれるんだからね、ってな感じです。
これが「ユークリッドの互除法」が最大公約数を導き出すことができる仕組みです。
この一連の操作、つまり正方形でスッと切って長方形をパタンを倒すという操作を数式で書くと以下のようになります。「663と816」の例を使いましょう。
最初の操作:
(816を663で割ると1あまり153)
2回目の操作:
(663を153で割ると4あまり51)
3回目の操作:
(153を51で割ると3あまり0:割り切る)
色を付けたのでわかるかもしれませんが、数値だけ見ると「左にズッとずらす」動きになっていますね。
この数を左にズッとずらす操作が、長方形を横に倒す操作と対応しているのですね。なぜなら、数を左にズッとずらすのも、長方形を横に倒すのも「割る数」を「割られる数」に、「あまり」を「割る数」にするという操作だからです。
ということで、ユークリッドの互除法が何をしているのかご理解いただけたでしょうか。
今回何の話だよって思うかもしれませんがここまでが前提です。さっそく本題に入っていきましょう。さっそくとは。
 と
と の最大公約数
の最大公約数
ある日、この長方形の図を眺めていて私はふと思ったのです。
「最大公約数」を求めるなんてのは、ふつうは整数とか自然数に対してしかやらない操作です。
しかし、「長方形」とかいうやつは、辺の長さが自然数でなくてはならない、なんてことはありません。例えば横が円周率(約3.14)、縦がネイピア数
(約2.72)であるような長方形だってあり得るわけです。
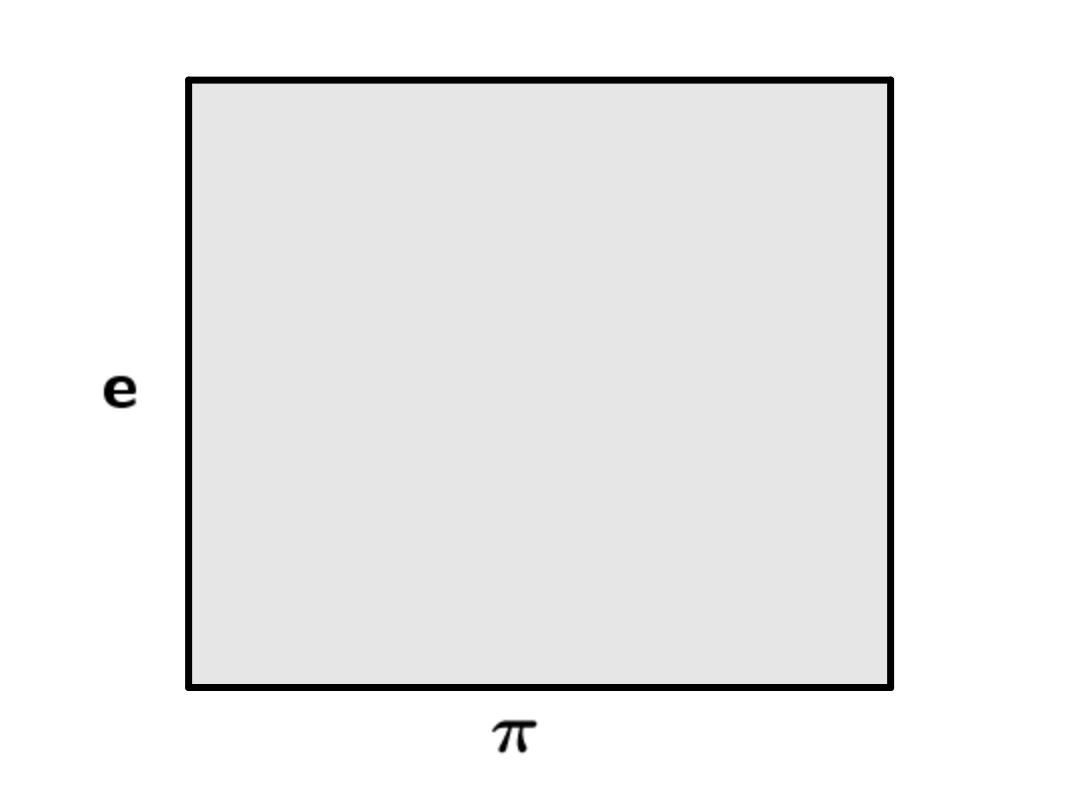
いや、別にと
じゃなくてもいいです。適当な無理数として特に有名なところから適当にピックアップしただけです。
そして、そんな長方形に対してでも「正方形で切り取れるだけ切り取る」「残った長方形を横に倒す」「それを繰り返す」という操作は行うことができます。だってこれらの操作ができることと辺の長さが自然数であることとは全然関係ないし。
であれば、実際それをやってみたらどうなるの? ということが気になります。こんなの全員気になるに決まっているのです。
つまりは横が円周率、縦がネイピア数
であるような長方形を使って、ユークリッドの互除法をやってみたい、ということ。
ここまでの話では、それをやると2数の最大公約数が求められるという話でした。しかし当然ながら、と
には最大公約数というのは存在しません。両方無理数だし。約数とかそういうのないし。
じゃあ本当にやってみたら何が出てくるんでしょうか。まあやってみるしかありません。善は急げです。
実際にやってみる
の長方形で正方形を切り取る操作をすると、まずは1つ切り取れます。
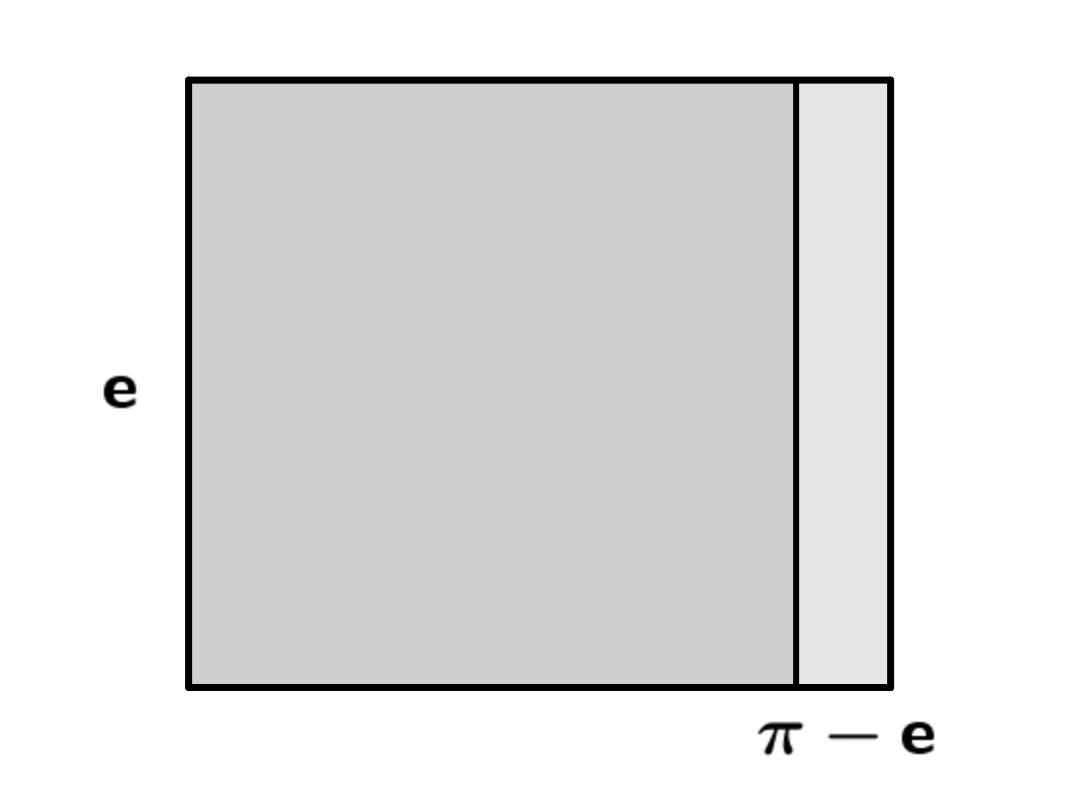
ここからいつものように残った長方形を横に倒す、正方形で切る、を繰り返していくと、
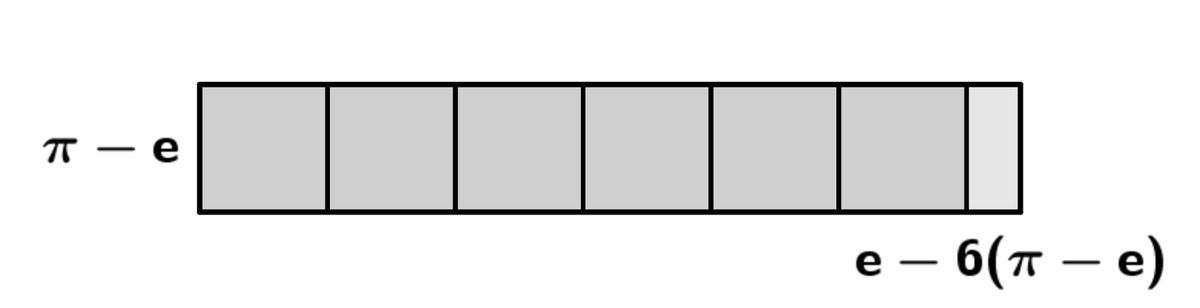
↓
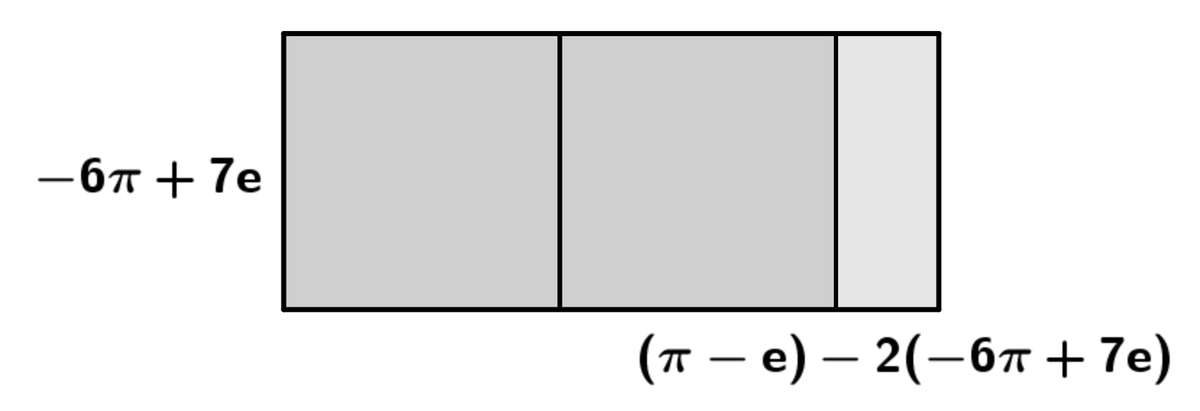
↓
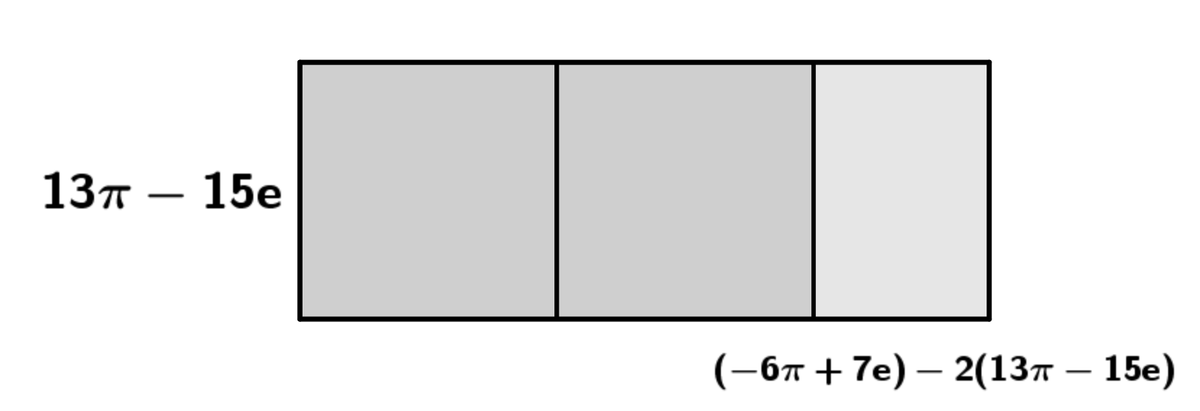
↓
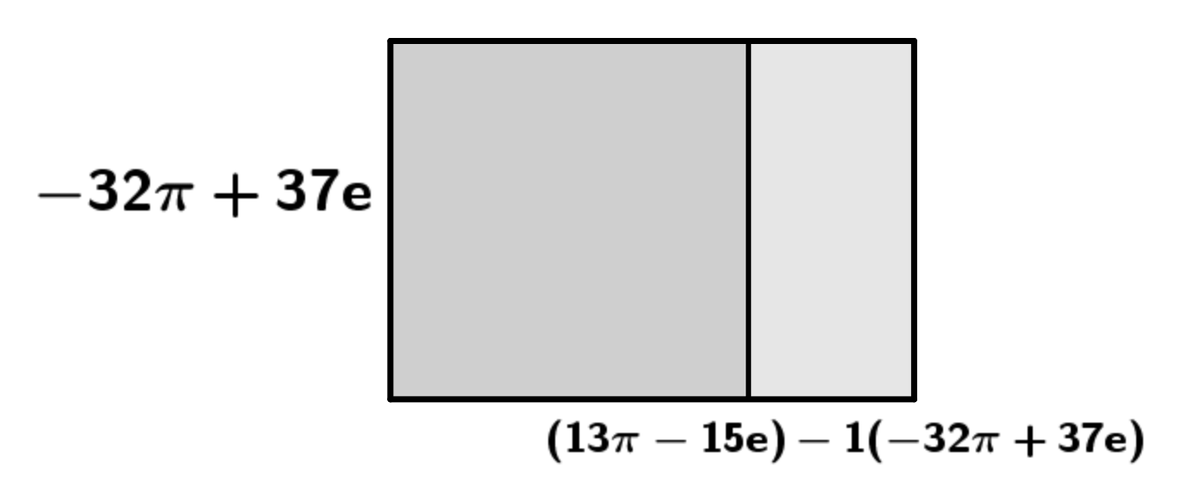
↓
……と、この先ずっと続きます。わかってはいましたが、まあ終わらないわけです。
と
とでユークリッドの互除法をやってみたら、終わらないことがわかりました。いかがでしたか? じゃないんだよな
もちろん、このままでは終われません。ということでここでちょっと見方を変えてみます。今までは無視していた「商」の方に注目してみるのです。
無視していたと言うと言い過ぎですが、今までは特に「あまり」の方に重きをおいて議論してきたわけで、「商」という従来は捨てていたおからみたいなやつに注目してみることで、なにか見えてこないか探りたいというわけです。
で、商というのは長方形の例えで言うなら「操作のたびに出てくる正方形の個数」のことです。今やった操作では上から順に1,6,2,2,1,2個の正方形が切り取られていますね。
そう考えると、と
でユークリッドの互除法をやった結果からは「1,6,2,2,1,2,…」という数列が出現したのだ、と捉えることができます。この操作は終わらないのでこの数列も無限数列になり、これ以降「6, 8, 2, 1, 1, 1, 4, 3, 1, 1, 66, 2, 1, 1, 2, 4, 2, 7, 46, 10, 2, 1, 18, 1, ...」と続きます。
この「ユークリッドの互除法をやると数列が出てくる」というのは別にと
に限った話ではありません。今までの結果を見てみても、
・「816と663」からは「1,4,3」という有限数列
・「767303と342516」からは「2,4,6,8」という有限数列
が実は出てきていた、とも捉えることができるんですね。
であれば、この「1,6,2,2,1,2,…」という無限数列に何かが潜んでいそうだと思えてきます。
じゃあこの数列って何なのかって話なんですが、この数列なんと実はですね、の正則連分数展開になっているのです。
連分数展開
連分数展開とは、見たことある方も多いかもしれませんがこんなやつです。
この形の分数を「連分数」といい、連分数の中で分子の部分が全部「1」になっているものを特に「正則連分数」といいます。「連分数」とだけ言って正則連分数のことを指すことも多くあります。
そして、何かひとつの実数をこの分数の形で書くことを「正則連分数展開」といいます。
正則連分数は、左側の数字の列だけで一意に(ただ一通りに)表すことができます。つまり、上の分数なら「1,2,3,4,5」といった具合ですね。これは分子を1に固定しているおかげです。
この連分数、かなりやばい見た目をしていますが、実は全然普通に計算することができます。「1,2,3,4,5」でやってみるとこんな感じ。
一番下の部分を通分して、
足して、逆数にして、
みたいなのを繰り返していくと、この分数は結局まで簡単にすることができます。恐るるに足らずって感じです。
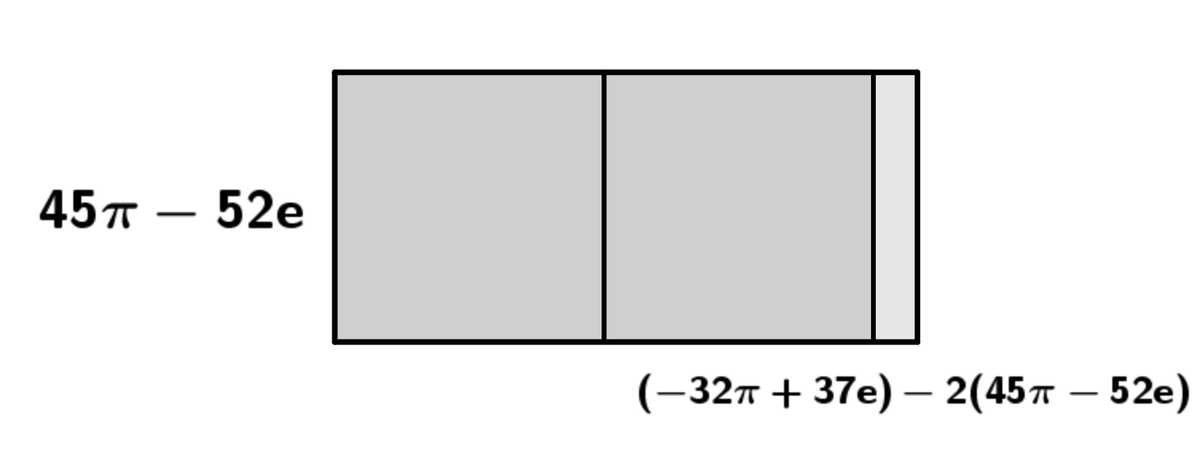
さてここで、この「225と157」で作られている長方形を考えてみます。
これに対してユークリッドの互除法を試してみると、こうなります。もう画像何個もあると作る方も見る方も大変なので一個の画像にまとめましょう。
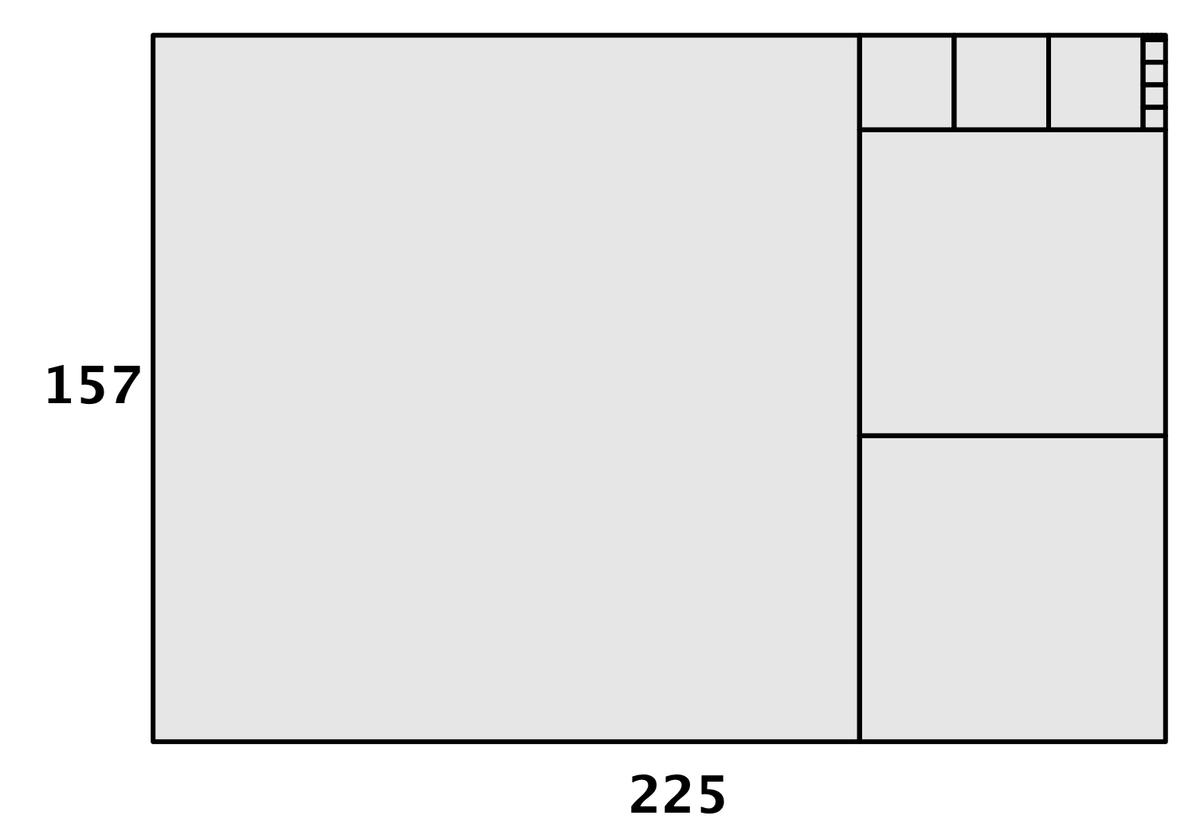
右上潰れていますがそこには確かに5つの正方形があります。
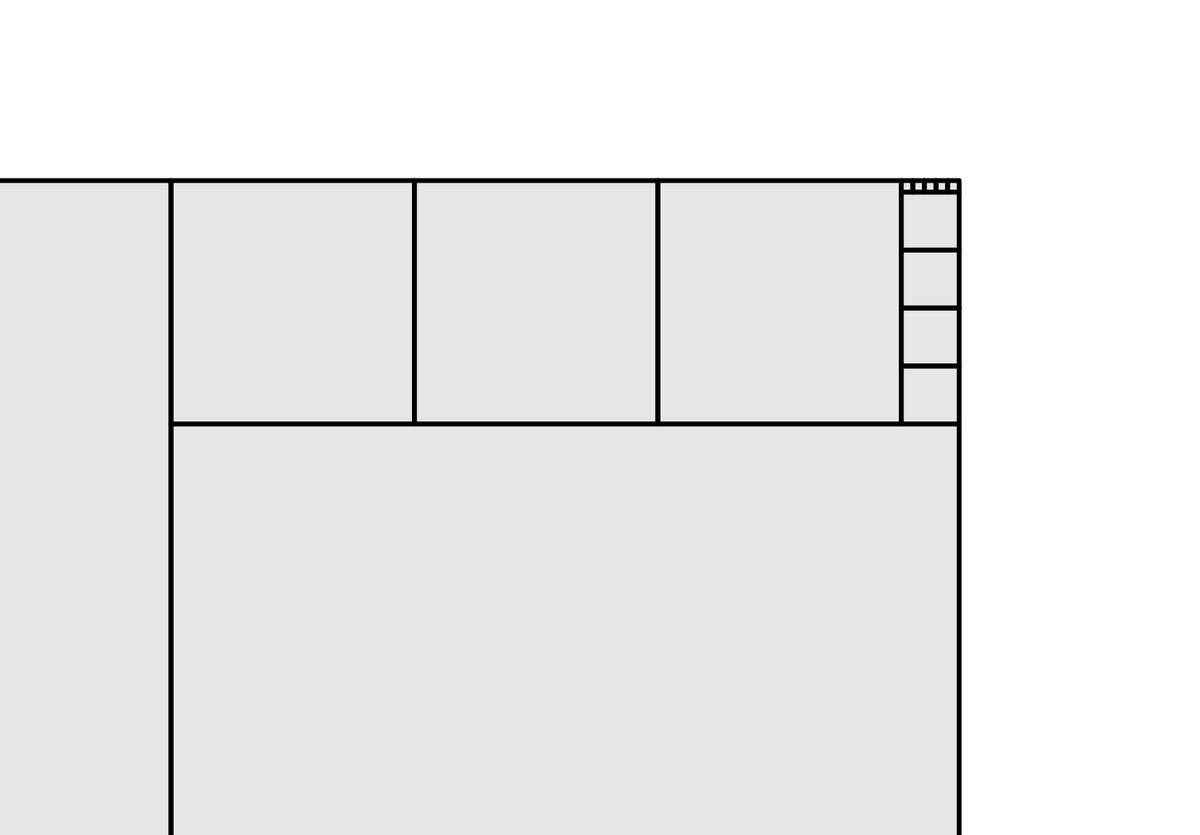
(右上を拡大)
ここに現れている正方形の個数を数えると、大きい順に「1,2,3,4,5」となっていて、それは確かにの連分数展開と一致しているんですねえ。ふしぎ。
互除法と連分数展開の数列が一致する理由
この理由を理解するために、まずはが連分数展開される様子を見てみましょう。ある数の連分数展開とは、「整数部分を取り出して」「残りの逆数をとる」の繰り返しで作ることができます。
は小数で書くと1.4331…となっていて、その整数部分は「1」です。この「整数部分を取り出す」というのは、式で書くならつまりこういうことです。
次に「残りの逆数をとる」というのは、つまりはこういうことですね。
単純に残った部分を「ぶんのいち」の形にしただけですね。
そしたら、今度はこの分母の部分で同じことをします。すなわち、また「整数部分を取り出す」「残りの逆数をとる」をやる。
の整数部分は2なので、この操作をやると、こうなります。
あとはこれをただ繰り返せば、の正則連分数展開「1,2,3,4,5」の完成です。興味のある方は自分でやってみるとよいでしょう。
さて。ね。
似てますよね?
2つの数の最大公約数を求めるやり方(ユークリッドの互除法)と、1つの分数の連分数展開を求めるやり方が。
どちらも「操作Aをする」「操作Bをする」「それの繰り返し」ということをしています。
実のところ、この
操作A:
・正方形を切り取れるだけ切り取る(互除法の方)
・整数部分を取り出す(連分数の方)
と、
操作B:
・残った長方形を横に倒す(互除法の方)
・残った部分の逆数をとる(連分数の方)
というのがそれぞれ対応しているのです。
2数a,b(a≧b)について、「正方形を切り取れるだけ切り取る(=a÷bの商を求める)」というのは、1つの分数について「整数部分を求める」ことと同じです。
同様に、「正方形を切り取れるだけ切り取って、残った長方形を横に倒す(=a÷bのあまりを求めて、「割る数」を「割られる数」に、「あまり」を「割る数」にする)」というのは、1つの分数について「整数部分を取り去った残りの、逆数をとる」ことと同じです。
これが、ユークリッドの互除法で出てくる数列が連分数展開で出てくる数列と一致する理由です。
2つの数に対して行うユークリッドの互除法は、その2数を分子・分母とする1つの数に対して行う連分数展開である、と言ってしまうとちょっと語弊があるかもしれませんが、やっている操作としてはだいたい似たようなものです。
いったんまとめておく
このブログは基本的に「高校卒業以来、一度も数学に触れてこなかった人」を対象にしているので、議論に使う道具についても基本的なところから説明しています。それが故でこの記事もかなり長くなってきてしまいました。ここまでの道筋をまとめておきましょう。
・2数の最大公約数は、それらを辺とする長方形をちょうど埋め尽くす正方形の一辺として表現できる。
・ということは、最大公約数を実際に求めるにはその正方形を見つける方法がわかればよい。
・それは、正方形で切り取れるだけ切り取る、残った長方形を横に倒して繰り返す、という操作で実現できる。
・その方法のことを「ユークリッドの互除法」という。
・ユークリッドの互除法は実際には、「長辺を短辺で割ったあまりを求める」「『割る数』を『割られる数』に、『あまり』を『割る数』にする」「それを繰り返す」、という操作のことである。
・最大公約数はふつう自然数でしか求められないが、「長方形」の話なら自然数かどうかとか関係ない。
・なので、と
の辺を持つ長方形に対しても、ユークリッドの互除法を適用させることができるはず。
・実際それをやってみると終わらないが、正方形の個数(商)の数列として「1,6,2,2,1,2,…」という数列が出てくる。
・この数列は、の正則連分数展開となっている。
・実数を連分数展開する操作と、2数の最大公約数を求める操作を比べると、確かにそれぞれの操作は一致している。
・なので、2数、
の最大公約数を求めようとすると、
の正則連分数展開が得られる。
と、いうことです。
いや〜まじか〜。まとめるとなんかめっちゃ長いですね! でもこれでようやく今回知りたかったことに一応の結論が出ました。
と
の最大公約数を求める操作をしてみたら、その操作は終わらなかったが、求める過程で出てきた数列は
の正則連分数展開を与えることがわかった。
ってことですね。
「あまり」に重きをおいて議論してきたのに、まさに「おから」みたいな副次的な産物だと思われた「商」こそが大事な存在として効いてきていてすごいね、という感慨があります。おから美味いもんね。
近似分数
これでこの記事を終えてもいいのですが、実はこの話はもう少し遊べます。
無限に続くの正則連分数展開「1,6,2,2,1,2,…」を途中で打ち切ったやつを考えてみましょう。
それは例えば「1,6,2,2,1」のことで、分数の形で書くと
ですね。これは計算するとです。
で、この分数一体なんなの?ってなると思うんですがこれ実は、「のとてもよい近似」を与えるのです。
実際、は1.155727…で
は1.155556…です。小数点第3位まで一致していますね。
今は連分数展開を「深さ5」までで打ち切っていますが、これは深さを深めれば深めるほど、つまり打ち切る位置を先にすれば先にするほど、近似の精度は上がっていくことが知られています。
深さ10まで採用したなんて小数点第7位まで一致しています。
だったらなんなのと思われるかもしれません。いやこれがすごいことなんですよ。だって、この近似分数ってと
をなるべく近くするような2数ってことじゃないですか。
と
は近いわけです。ということは必然的に、「45
と52
は近い」ということになります。それぞれ141.371…と141.351…です。確かに近い。19791
と22873
なんてもっともっと近いです。
これ、なんだかよくないですか。どちらも無理数どころか超越数であると
は、どれだけ自然数をかけても一致するということはありえないわけです。
しかし、この連分数展開で得られた自然数のペアなら、2数が一致することはないけれどもいくらでも近づけることはできる。
「自然数倍」という操作では交わり得なかった二人が、連分数展開という協力者によっていくらでもその距離を近づけていくことができる……。
なんとなくエモみを見出してしまいました。まあたまにはこれくらいウェットに数学やってもいいでしょう。
おわりに
今回の結論は、
と
の最大公約数は見つけられなかったが、見つけようとする過程で
と
を限りなく近づけるような自然数のペアは見つかった。よかったね。
といった感じです。ハッピーエンド。
何に使えるかとかはよく分かりません。気になったからやってみただけです。別になんにも使えなくてもいいと思います。なんかに使えたら使えたで、それはそれで儲けもんでしょう。数学ってだいたいそういうもんです。
それでは今回はこのへんで!
(大事な追記)
えー……。うゔん、あっ、あのー……。
この記事公開後に教えてもらったんですがが無理数かどうかは証明されていないらしいです。
これはこの記事にとっては致命的です。この記事では「の連分数展開は終わらない」ことを前提として話を進めてきました。
が無理数かどうかは証明されていないということは、これの連分数展開が途中で終わっちゃう可能性があるということです。
いやー。ね。参りました。うっかりでした。も
も無理数だから何も考えず使いましたが、まさかわかっていないなんて。
でももしが有理数だったら
の形で書けるってことなので、なかなかそんなことはなさそうに思えます。
とはいえ、それはちゃんと証明しなければならないことです。
あ〜。記事の大改造するの手間だな〜
なんか急にの無理性を証明したい機運が高まって明日あたり証明されたらいいのにな〜
