国名がつく数学用語っていくつかあって、「日本の定理」とか「ポーランド空間」とかあって面白いんですが、なかでも中国剰余定理というのは特に有名です。
で、こいつが数論ではまぁ〜非常によく登場する重要な定理なんですね。
そのステートメントは例えばwikipediaにはこんなふうに書かれています。
与えられた k 個の整数 がどの二つも互いに素ならば、任意に与えられる整数
に対し
…
を満たす整数が
を法として一意的に存在する。
はい。うん。ね。いやもちろんこれで分かる人にはいいんですが。
中国剰余定理の拡張や応用には色々と面白い話題があって、ググったりなんかすると百花繚乱といろんな話題が出てきます。しかし、この定理を「まず理解する」というだけでもつまづいてる人というのはいるのであって、この記事はそんな人のための記事です。
まあだいたいアジマティクスっていつもそんな感じです。これ↓とか。
さて、プログラミングやら整数論やらでよく出てくる「中国剰余定理」、こいつの正体とは一体何なのでしょうか?
まずはとても当たり前の話からしましょう。当たり前のことから積み上げていくのが理解というものだからです。
とある表
次のようなことを考えてみます。
数を0,1,2,3,4,…と数え上げていくとき、それぞれの数を3で割ったあまりを考えるのです。
「0」を3で割ったあまりは0、「1」だとあまりは1、「2」は2、「3」でまた3で割ったあまりは0になって、これはぐるぐるとループします。
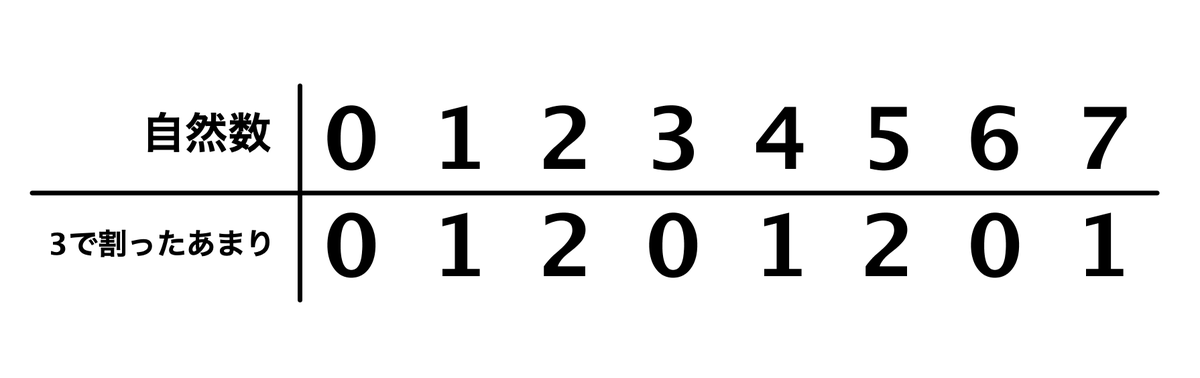
まあ、言われてみればそれはそうなんですが、そんなに意識したことのなかった人も少なくないかもしれません。
もちろん、これは3だけに限った話ではなくて、例えば5だと「0,1,2,3,4」のループとなります。一般に自然数nにおいて「nで割ったあまり」を考えると、「0〜n-1」のn個の数のループとなります。
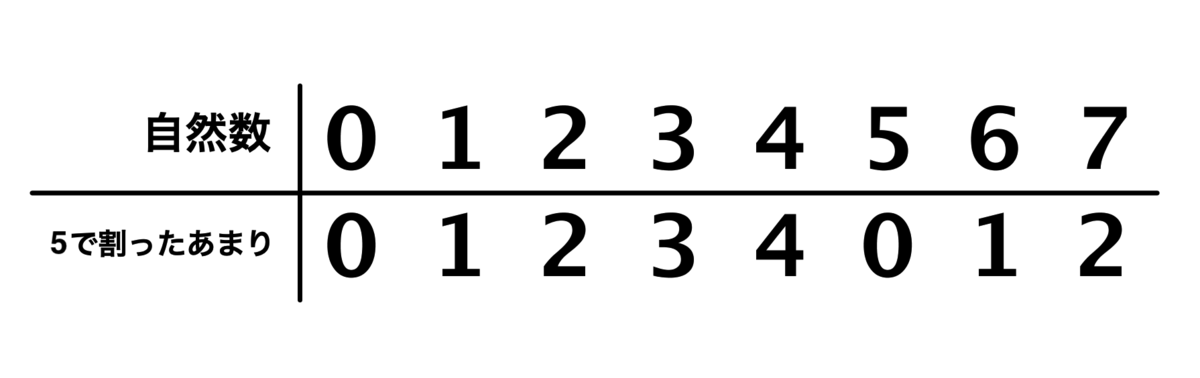
さて、ここでこんなものを考えます。
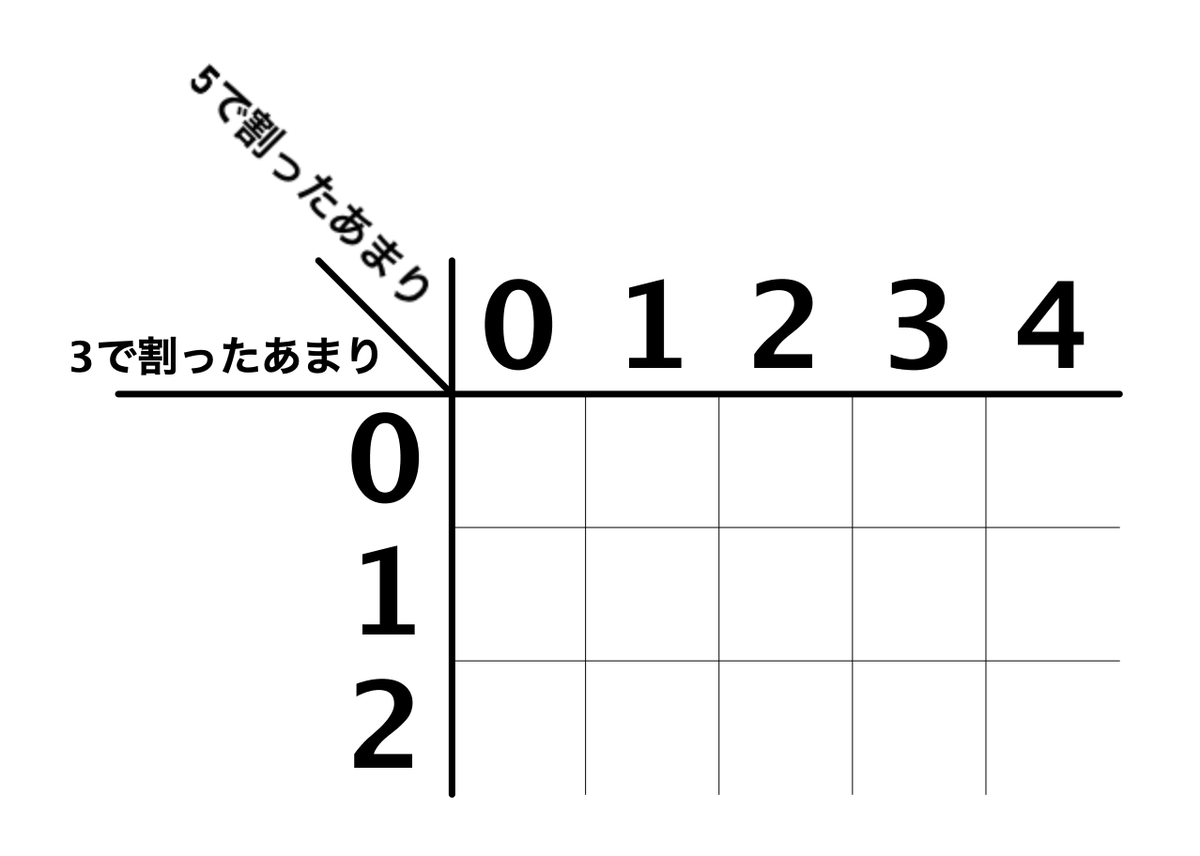
縦軸に3で割ったあまり、横軸に5で割ったあまりをとって表にしてみたわけです。この表の空欄に、自然数を入れることを考えます。
例えば「7」という数は、3で割ると1あまり、5で割ると2あまるため、
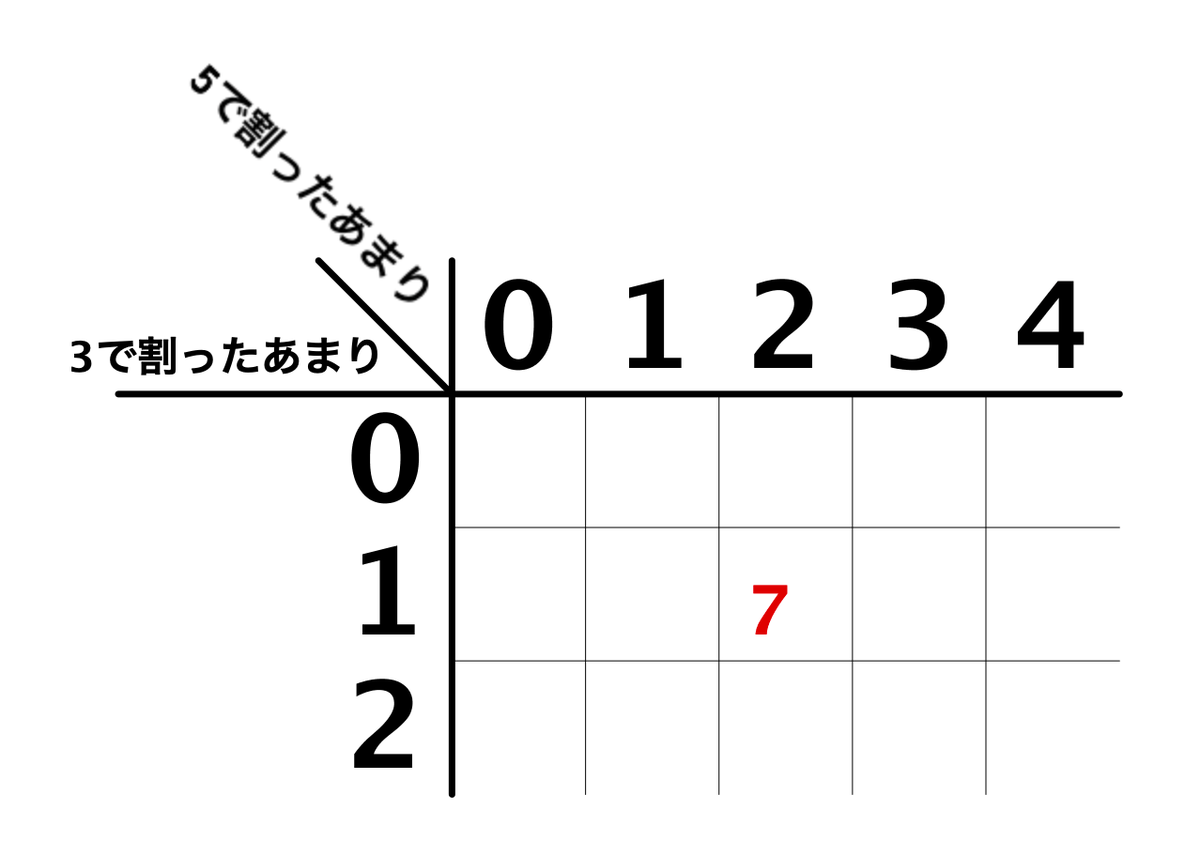
この部分に入ります。……ということをするための表なわけです。
ここには3×5で15個のマスがあるわけですが、じゃあってことでこの表に0〜14までの15個の数を入れることを考えてみます。
まず、0は3で割っても5で割ってもあまりは0なため、ここに入ります。

これ以降も同様で、1,2はそれぞれここに入ります。
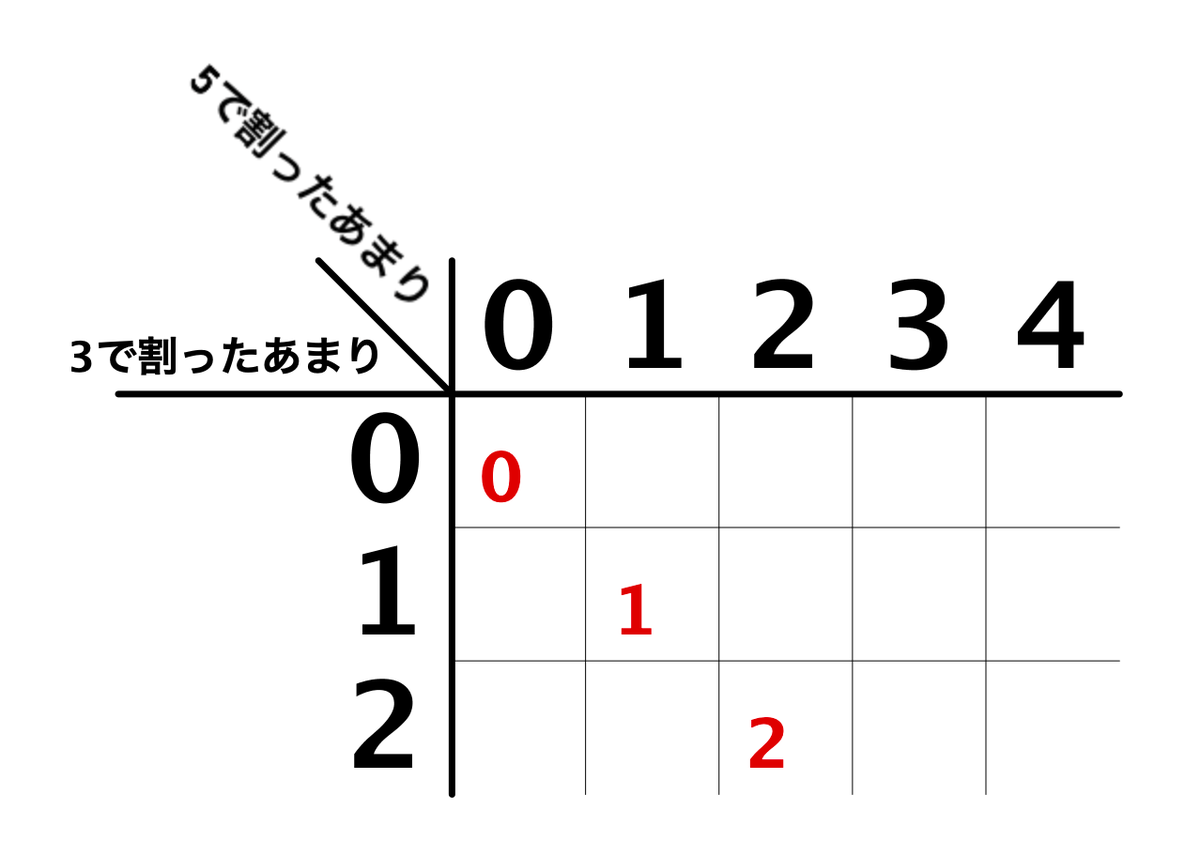
ナナメに伸びていく感じになるのですね。
「3」でちょっと変わって、3を3で割ったあまりは0ですが、5で割ったあまりは3なので、ここに入ります。
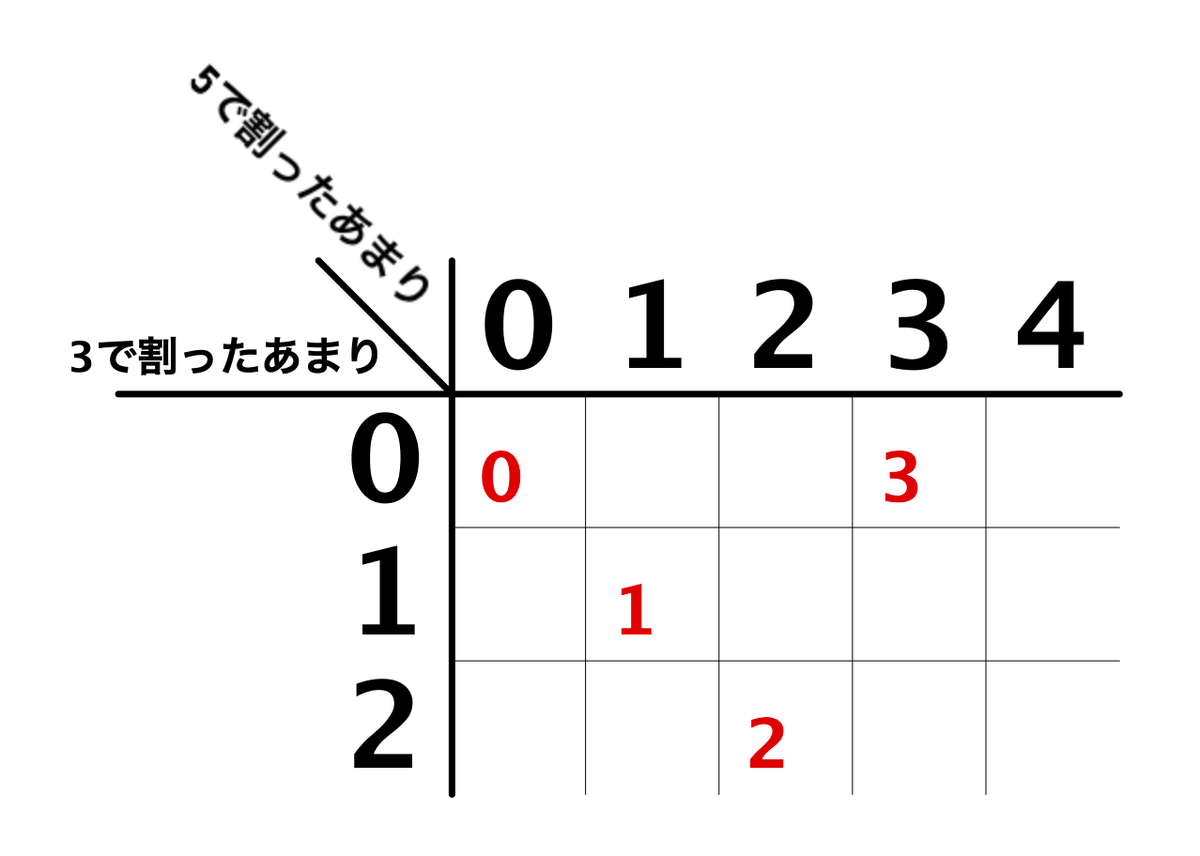
昔のゲームのマップみたいに、上下の辺でワープしている感じになるのですね。これはさっきの「あまりがループしている」という話と対応しています。
そして、このまま続けていくと以下のようになります。
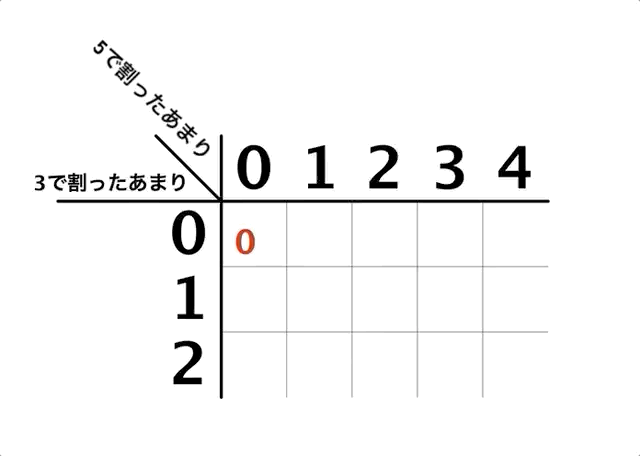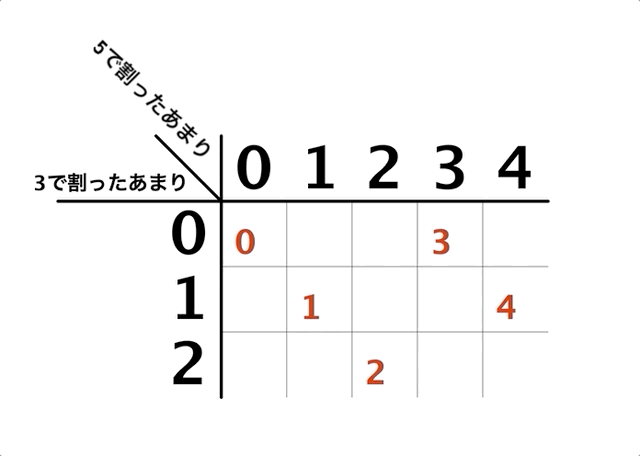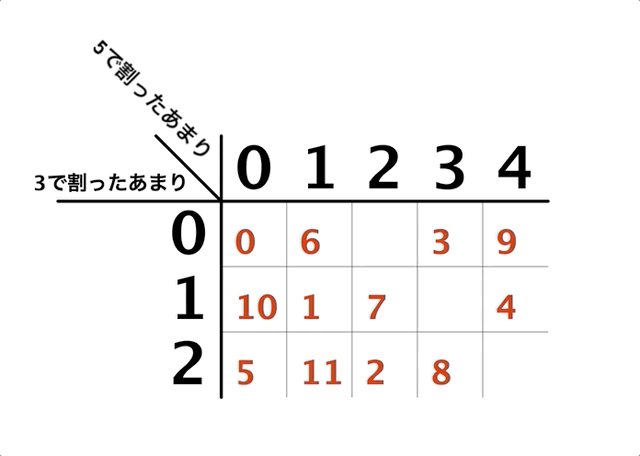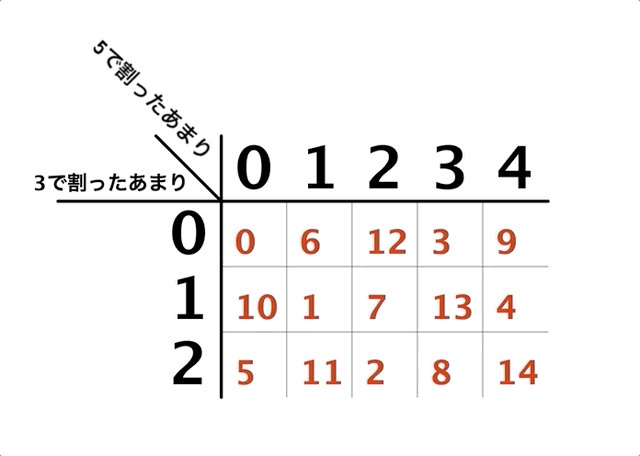
へえ〜
3と5で割ったあまりを表にして、できた15個のマスに0〜14の数を入れていくとき、漏れもダブりもなくすべてのマスを埋め尽くす、ということが見て取れますね。
ところで、「0〜14の数」というのは、ある数を「15で割ったあまり」として出てくる数そのものです。
なので上記の「マスを埋め尽くす」というのは、見方を変えれば「3で割ったあまりと5で割ったあまりとのペア」と、「15で割ったあまり」が一対一対応している、という風に捉えることもできるでしょう。
(2,1) ⇔ 11
(0,4) ⇔ 9
(1,0) ⇔ 10
などなど。みたいな。
「ある数を3で割ったあまりの情報と5で割ったあまりの情報とを両方調べれば、その数を15で割ったあまりの情報もわかる」と捉えてもいいかもしれません。逆もしかり。
そして実のところ、これこそが中国剰余定理そのものなのです。
中国剰余定理
まあ「そのもの」というのは言い過ぎです。だっていまのところ「3と5」と「15」っていう具体的な数の間の話でしかないし。
ちゃんと一般的に言うなら、こんな感じです。
互いに素な2数nとmにおいて、「nで割ってaあまる数」と「mで割ってbあまる数」というのを同時に満たすようなnm未満の数(0〜nm-1)は、必ず存在して(漏れがない)、しかもちょうど一つだけ存在する(ダブりがない)。
捉えにくいですか? 図に合わせた説明をするなら、こうなるでしょう。
互いに素な2数nとmにおいて、0〜nm-1の数を「あの表」に埋めていくことを考えると、空いたマスは存在せず(漏れがない)、しかも一つのマスに2つの数字が入ることはない(ダブりがない)。
上の図を見ればすぐですが、文章で説明するとやっぱりちょっと煩雑になってしまいますね。
それでも、冒頭のwikipediaの言及と比べて、ずいぶん捉えやすくなった感じがするのではないかと思います。
付け加えると、いまは「2数」としましたが、この定理は2数には限りません。3つ以上の数、例えば3で割って2あまり、5で割って3あまり、さらに7で割ったら2あまるような数は、3×5×7 = 105未満の数の間にちょうどひとつだけ存在する、ということが中国剰余定理から実際に示すことができます。
互いに素
さて、ここで「互いに素」というのは重要です。互いに素とは、2つ以上の数についてそれらが「同じ素因数では割り切れない」ということを意味します。
10と7は互いに素。6と15は互いに素ではない(どっちも3で割り切れる)。
で、2つの数に共通の素因数があったりする場合(互いに素でない場合)には、中国剰余定理はうまくいかなくなってしまうのです。
どううまくいかないかといえば、互いに素でないときは「漏れ(空いたマス)」も「ダブり(数がダブって入ってるマス)」も、両方出てきてしまいます。
実際に一つ例をとって見てみましょう。例えば「3」と「6」。6が3で割れるので明らかに互いに素ではありません。

一目瞭然ですね。「漏れ」も「ダブり」も、両方出てきてしまっています。
「漏れ」に関して言うと、例えば「3で割って1あまり、6で割って2あまる数」というのは存在しません。空欄になっていますね。
「ダブり」に関してだと、例えば「3で割って1あまり、6で割って4あまる数」というのは、3×6=18までの間に4,10,16と3つも登場してしまっています。
別の例でも見てみます。「10」と「6」とかだとこう。
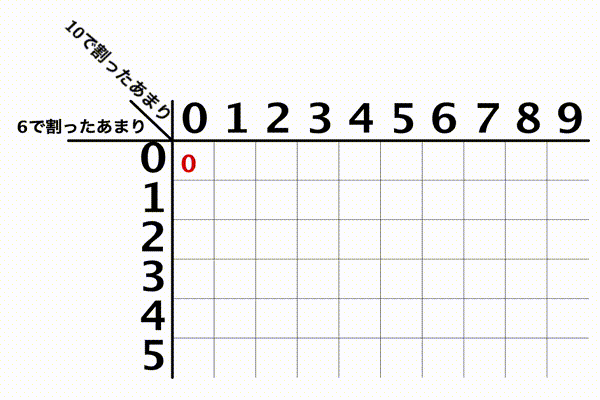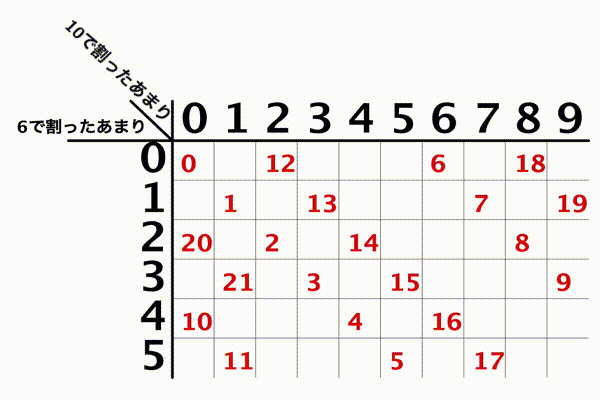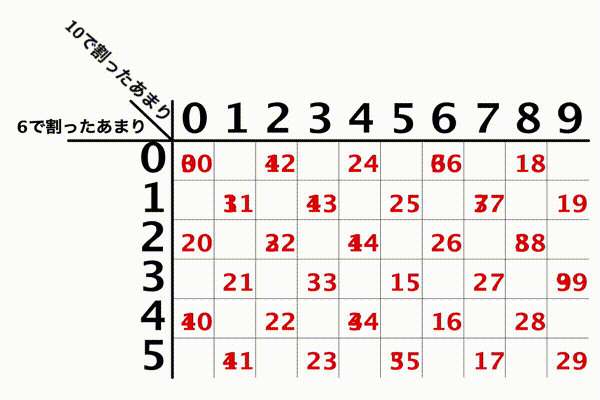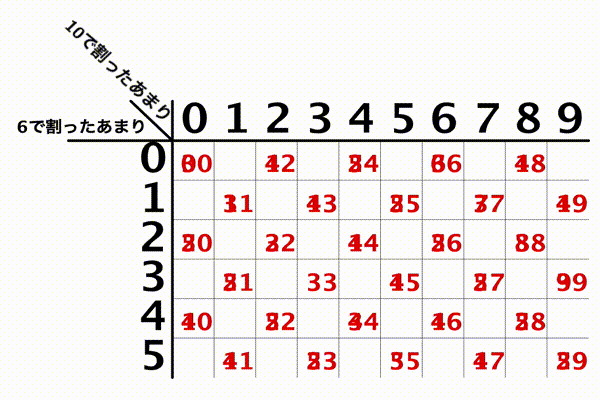
ね。
中国剰余定理が保証する「漏れもダブりもない」というのが、いかに特別なことであるかおわかりいただけるかと思います。
ということで、これが中国剰余定理というものの「姿」だったわけです。
図だけ見てるとやけに直感的というか自明感の強い定理に見えるかもしれません。
「直感的には明らか感強いけど、数式で厳密に表現しようとするとけっこう大変」な定理であって、その上で「先に数式で厳密に書かれたほうを知った」場合、もとの直感的な明らかさって、あんまり得られなそうに思います。
そういうの往々にしてあると思うんですよね。数学って。中国剰余定理とはその最たる例だと思います。
でもまあ、恐るるに足りません。中国剰余定理とはこういう姿をした定理だった、というだけのことなのです。
答えを直接求めてくれるわけではない
一点、大事なことに触れておかねばなりません。
ここまでさんざん説明してきたことですが、中国剰余定理とは「3で割って1あまり、5で割って2あまるような数は0〜14の中にちょうど一つだけ存在する」というようなことを言う定理でした(これは一つの例ですが)。
つまり、この定理だけではその「ちょうど一つ」というのが実際何の数なのかには答えてくれないということです。
しばしば「3で割ると2あまり、5で割ると3あまり、7で割ると2あまる数は何か、という問題は、中国剰余定理で解くことができます」などといった説明を見かけることがありますが、まあ間違っているというわけではないですが説明としてはちょっと微妙です。
中国剰余定理はこれの解の存在を保証しているだけなんですね。
実際にそれを計算するには、拡張ユークリッドの互除法とか、ベズーの等式とか、また別の道具立てが必要になってきます。
それはそれで記事として書くならひと記事分くらいの分量になってしまうので、やるならまた改めてということになるでしょう。
というわけで今回は、数論やる上で避けては通れない中国剰余定理の紹介でした。
白状しますと、私自身は「中国剰余定理を使うことにより簡単に解けるようになる問題」みたいなのってそんなに知らないんですよね。避けては通れないとか言っておきながら。
よくあるのは「中国剰余定理により解が一意である(一つだけである)ことが保証されているので、それを求めればよくて……」みたいな流れで出てくるタイプです。
そう考えると、中国剰余定理というのは数学における「縁の下の力持ち」的な立ち位置なのかもしれませんね。
派手な活躍はしないけれども、気づけばいつもそこにいる……。
人間、できるならそうありたいものです。
何の話?
それでは今回はこのへんで!
