神様。この記事にうさんくさ自己啓発本みたいなタイトルをつけることをお許しください。
数学のつまずきポイントは人それぞれいろいろあると思いますが、高校で出てくる「ラジアン」や「弧度法」とかいうやつが鬼門だったという人、少なくないのではないかと思います。
かいつまんで説明しましょう。我々は角度を表記するのに「度」という単位を使った「度数法」で表記することが多いですが、「度」の代わりに「ラジアン」という単位を使ったものが「弧度法」です。
例えば、度数法でいう「135°」は弧度法では「ラジアン」、「72°」は「
ラジアン」となります。
それだけ聞くと、知らない人や忘れてる人からすればなにそれ、ってなるのは当然だと思います。
かくいう私も、いままで平然と「ナニナニ度」と呼んできたものがいきなり「うんちゃらパイ」などと呼ぶようになって、ラジアンを習った当時は面食らったものです。
当時は根本的な理解をしていなかったし、大人になってからも度数法を弧度法に変換するやり方は毎回忘れて毎回ググってました。「当時は」どころか最近まで根本的な理解をしていなかったのですね。
というわけで、この記事は高校で習ったはずの「弧度法」「ラジアン」の本質的な理解を目指す記事です。
重ね重ね、この記事にうさんくさ自己啓発本みたいなタイトルをつけることをお許しください。神様。お願いだから。
(ボツ案)
・長生きしたければ「π/180」を使うのをやめなさい
・フランス人の9割は「π/180」を使わない
・人生で大切なことはみんな弧度法が教えてくれた
弧度法・ラジアンとは
実はこれ、全然難しいことじゃありません。いやほんとにまじで。
角度って、「円一周の何分の一か」みたいなとこあるじゃないですか。180°は円一周ので、90°だったら
、みたいな。円グラフを想像するとわかりやすいと思います。

で、実際に180°のことを「」、90°のことを「
」って表現したとしたら、これってつまり「一周を1としたときの割合で角度を表現している」ことにほかならないわけじゃないですか。
そして、別に「一周を1とする」ことにこだわる必要はないわけですよ。例えば一周を「360」としてみて、その割合で角度を表現してみるとか。360って約数多くて便利そうだし。
これが「度数法」です。すなわち「一周を360としたときの割合」で角度を表すのが度数法。
なので、一周を1としたときに「」と表現されていた角度は、
かける360で90°となります。
そして「一周を360としたときの割合で表現していますよ」ということを明示するための単位として「度(記号:°)」を使うわけです。
さて、一周を何としてもいい、ということだったので一周を「」としてみて角度を表示したものが、すなわち弧度法です。
弧度法でいう90°はラジアンとなります。つまり、
(全体)に
(割合)をかけたもの。
同様に、135°なら一周のなので(
を約分しただけ)、弧度法では
かける
で
ラジアンとなります。
それだけ。本当にそれだけのことなんです。ただ単に全体が360なのかなのかという違いだけ。
それだけのことなのになぜ弧度法やラジアンに「わかりにくい」みたいなイメージが付きまとっているか。それはやはり「なぜなの?」という部分が置き去りにされてしまっているからでしょう。
これを納得するには、「角度とは何か」という疑問に踏み込まなくてはなりません。
角度とは
角度というものを知らない人はいません。だいたい「同じところから出る2つの線の開き具合い」みたいな感じで理解している人が多いだろうし、日常会話で使うだけならそれで問題は発生しないでしょう。
しかしそれを数学で使えるようにちゃんと定義するとなると、話は別です。角度は数学的には、こんな感じで定義されています。
共通の一点Oから出る2つの線分について、
その一点Oを中心とする円を考えたとき(これを「円O」とでも呼びます)、
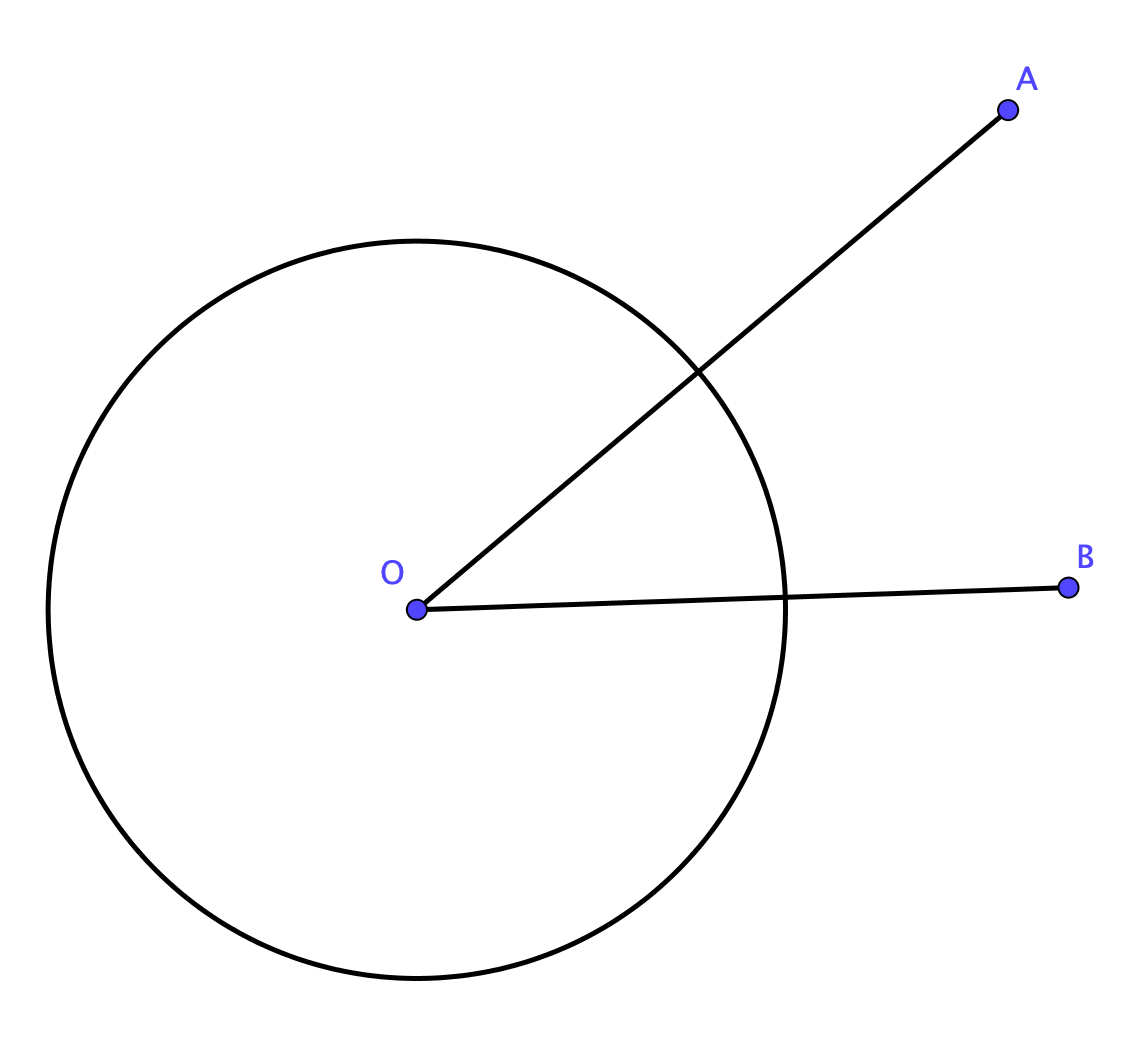
この円Oの「半径」と「2つの線分が円を切りとった弧の長さ」との「比」
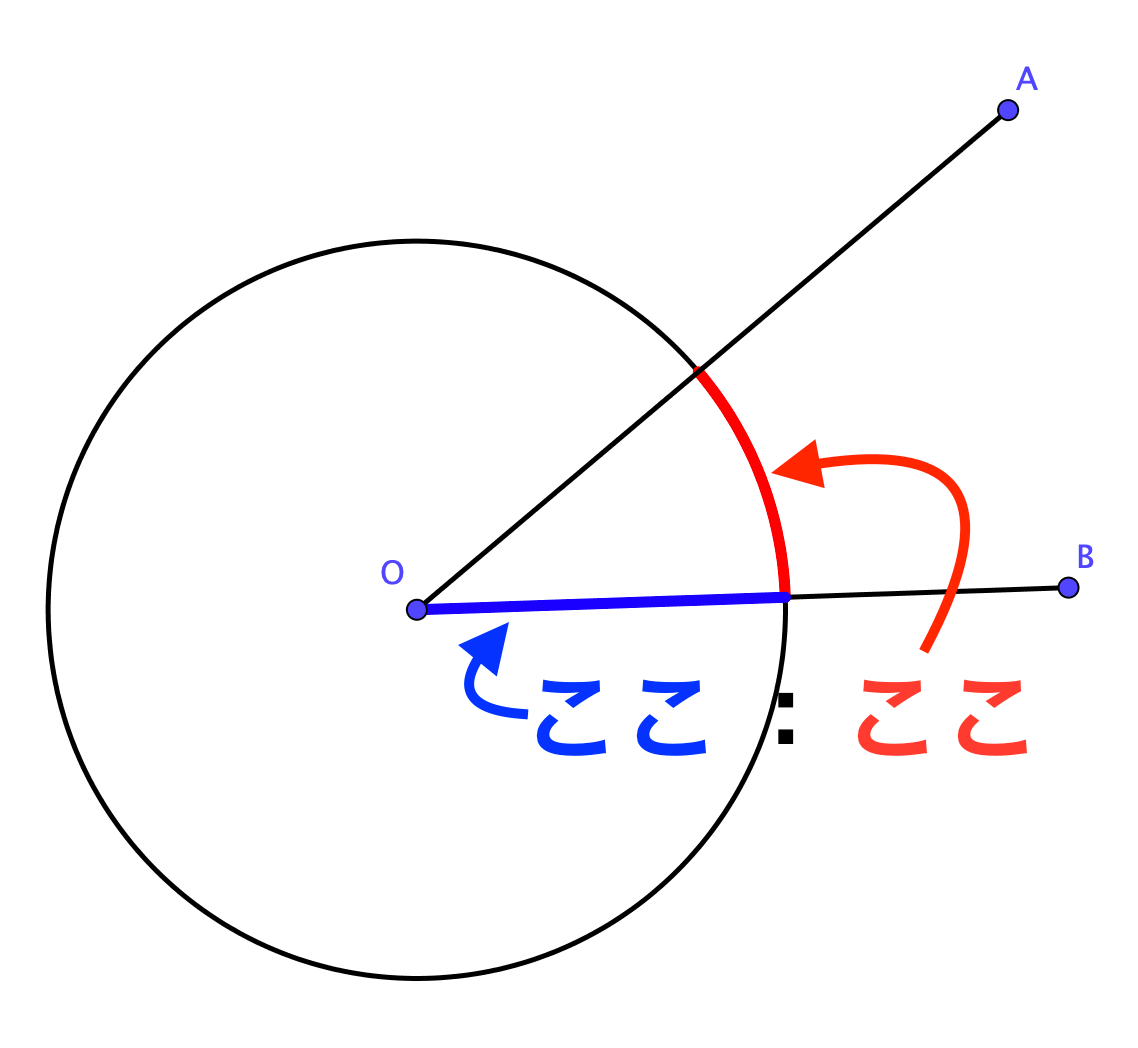
として、角度は定義されているのです。
なんだかよくわかりませんね。「半径と弧の長さの比」という言い方は少し捉えづらいので、同じ意味の別の言い方をしておきましょう。
角度とは、「円Oの半径が1のときの、2つの線分が切り取る弧の長さ」です。
これらが同じ意味であることはわかると思います。一般に「AとBとの比」というのは、「Aを1にしたときのBの値そのもの」だからです。ここではAが半径、Bが弧長ですね。
つまり、ここまでの話の帰着として、角度とは単に半径1の円の「弧長」のことである、ということになりました。
この定義は、我々のもつ角度というものへの直感的な理解をよく反映しているのではないかと思います。2つの線の開き具合を測るには、単にその間の弧長を計測すればいいだろう、という。
さて、この弧長って円全体で測るとですよね。小学校で習う、以下の公式そのものです。
円周の長さ=円周率×直径
いわゆる(にーパイアール)というやつです。半径を
とおいているので、
が直径。
が円周率。いまは半径が1の円のことを考えているので、一周は
。
これを「どれだけ切り取るか」で角度は定義されているため、弧度法が採用している「全体をとする」には合理性がある、というわけなのです。
※合理性はあるけど実際に使う理由は…?となるかもしれないけどその理由もちゃんとある。微分したときに余計な係数が出てこないとか。
度数法と弧度法の変換
さて。不肖わたくしが今回の記事で最も言いたかったことはここからです。
度数法で表示された角度を弧度法での表示に変換したい、という場面はよくあります。225°ってラジアンだといくつだっけ、といった具合に。
そしてそれについて、以下のような言い方がしばしばなされます。
・度数法を弧度法に変換するには、度数法の値にをかければよい。
もちろんこれはまったく正しい言明です。しかし、これもう、ほんともう、この言い方では本質の見えなくなり具合がすごい。なんですか? とかいう値は。
度数法を弧度法に変換するにはどうすればいいかちょっと考えてみましょう。
まずは変換したい値が全体のどれだけの割合であるのかを求めます。度数法における「全体(円一周)」は360だったので、例えば225°で考えるならそれにをかけた
を計算すればよい。
これは約分するととなって、225というのは360の中では
の割合にあたることがわかります。
それを弧度法にするには、「の中での
の割合」とはどれくらいにあたるのか計算すればよくて、
で225°
ラジアンと求まるわけです。
やってることは「換算」という計算が発生するときにいつもやっていることにすぎません。
日本国民1億2650万人のうち東京の人口は約1400万人(2021年1月1日現在)。1クラス30人のうちだったらどれくらいにあたるだろう、というのを計算したいとします。
この場合まずを計算して東京人率を求めて、それを30にかけて約3.3を得るわけですよね。
・日本の東京人率は1クラスで言うと3.3人
・度数法の225°は弧度法で言うとラジアン
この2つは本質的には全く同じことをやっているのです。
というわけで、弧度法への変換をひとつの言い方でまとめるならば、こうなるでしょう。
・度数法を弧度法に変換するには、度数法の値にをかけて、そして
をかければよい。
当然、は計算すれば結局
と同じなので、ちゃんと理解しているならば
を使ったほうが計算は速いです。
しかし、「弧度法への変換はをかければよい」とだけ覚えていると、その本質的な意味を忘れてしまいがちなんですね。本質的な意味を忘れて毎回ググるような奴に堕してしまいがちです。
思考停止状態で「をかける」と覚えるのは辞めて、「
をかけて、そして
をかける」と覚えておくと、ただ換算ができるようになるだけでなく、弧度法やラジアンへの本質的な理解も深まるだろうと、個人的には思うのです。
おわりに
数学ってけっこう「捉え方の学問」みたいなところがあります。ああも捉えられるけど、こうも捉えられるよね。同じことだけど。みたいな。
「をかける」と「
をかけて、そして
をかける」は数学的には完全に同じですが、人間の捉え方としては異なります。
同じことだけど、ああやって捉えるよりこうやって捉えたほうが理解がしやすかった、というのは、数学をやっているうえで幾度となく経験することです。
ただ教科書の記述を写し取るのではなく、自分なりの「捉え方」を試行錯誤しながら数学をやってみると、また違ったものが見えてくるのではないかと思います。
それでは今回はこのへんで!