群を見る会 - アジマティクス

以前、現代数学に欠かせない道具である「群」とはなんなのかについての記事を書きました。

www.ajimatics.com

群とは、解像度の低い順に言って、次のようなものでした。

・構造の一種

・「集合」と「演算」で出来ている構造の一種

・「閉じている」「単位元がある」「逆元がある」「結合則を満たす」という条件を満たす集合と演算の組

しかしこれがわかっただけでは、「なんでそんなもの考えるの？」という問いには答えられていないように感じます。

なんで群なんてものを考えるのか、その大きな理由の一つは「構造自体を調べたいから」にほかならないでしょう。

一見違う現れ方をしている二つの概念が、構造として見たら実は同じであった。となれば、その構造自体を調べたいと思うのは自然なモチベーションだと思います。

というわけで今回の記事では、そんな群のさまざまな例を「アレとコレとが実は同じ」という点に着目して紹介していきます。

一つ一つ定義を確かめる、などのことはこの際抜きにして、「アレとコレが同じなんてすごいね〜〜〜」ってことを鑑賞するための記事だという趣旨ですので、ご理解の上お付き合いください。

例１：旗揚げゲーム・長方形・オメガ

旗揚げゲーム

「赤上げて」「白下げて」などの命令を正しく遂行する「旗揚げゲーム」というのがあります。

あの旗揚げゲームにおいて、今回は「上げて」「下げて」ではなくて「上がっているなら下げ、下がっているなら上げる」ということを表す「変えて」という命令を使うことにします。

そして「赤変えて」「白変えて」「両方変えて」「変えないで」という4つの命令でこのゲームをやることを考えましょう。

その上で、ここに「2つの命令を連続してやる」という演算を導入します。

そうすると、「赤変えて」+「白変えて」は「両方変えて」と同じだし、「両方変えて」+「白変えて」は「赤変えて」と同じことだとわかります。

数学的な話ではありません。実際に右手に赤、左手に白の旗を持って、「両方変える」ということをしたあとに「白だけ変える」ということをすると、結果として見れば「赤だけ変えた」のと同じことになるね、というだけのことを言っています。

これらの関係を表にすると以下です。

f:id:motcho:20200421112202p:plain

もうおわかりかとは思いますが、この4つの命令の集合は「2つの命令を連続してやる」という演算のもとで群をなします。

すなわち、閉じていて、単位元とそれぞれの逆元が存在して、結合的な構造を持ちます。

長方形の合同変換

以前の記事では「正方形における、形を変えないような操作」を扱いました。じゃあってことで今回は長方形に対しての形を変えない操作のことを考えます。

形を変えないような操作とは、いわゆる「見ている人が目を閉じてる間にやっても気づかれないような操作」ってやつですね。

f:id:motcho:20191204054337p:plain

そして、以前の記事では「裏返し」を認めていませんでしたが、今回は裏返しも認めることにします。

そうすると、長方形の「かたちを変えないような操作」とは、「なにもしない」「180°回転」「縦方向に裏返す」「横方向に裏返す」の4種類だけになります。

f:id:motcho:20200421101521g:plain

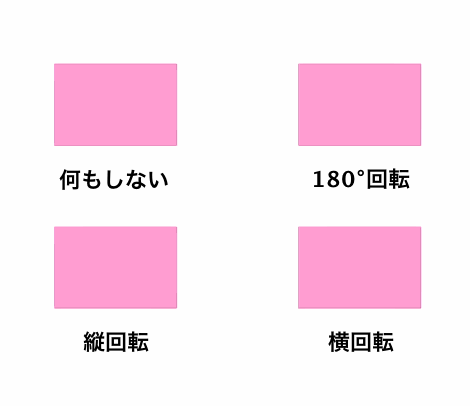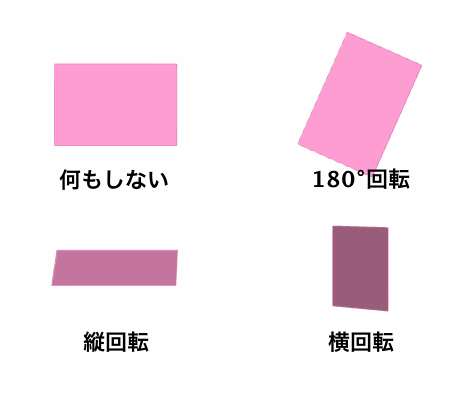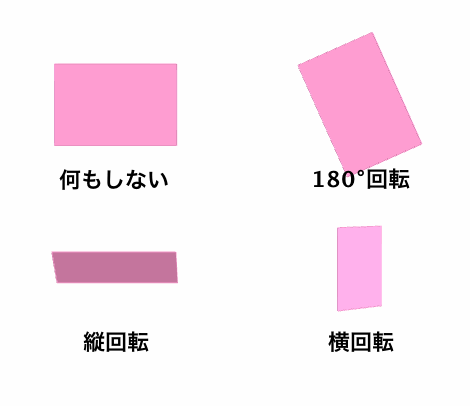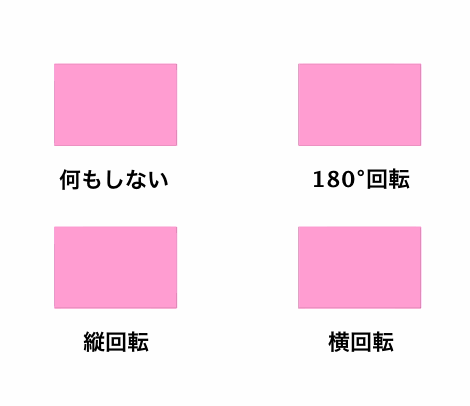
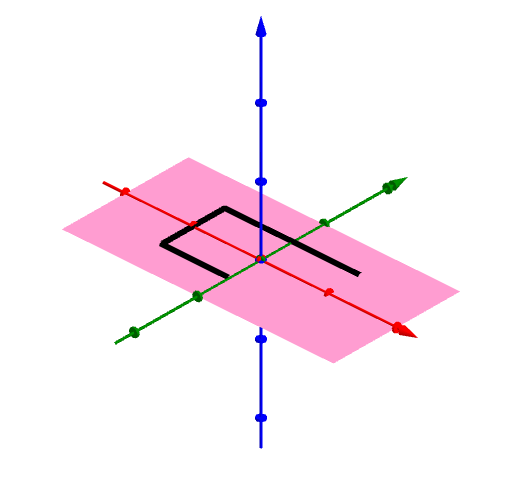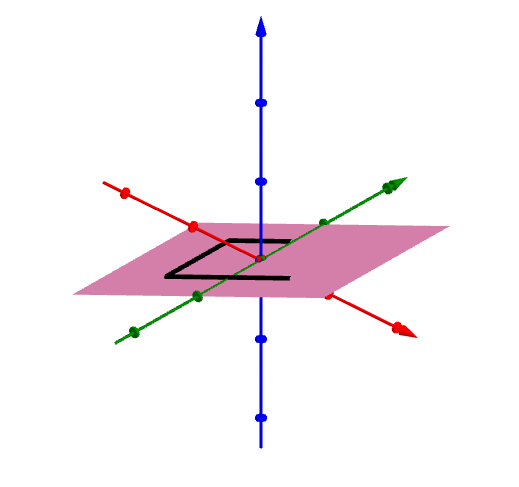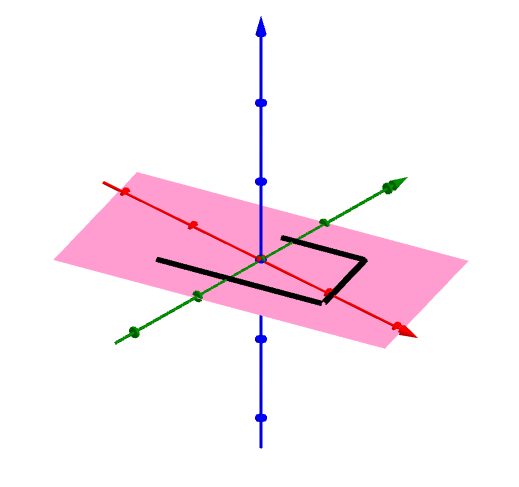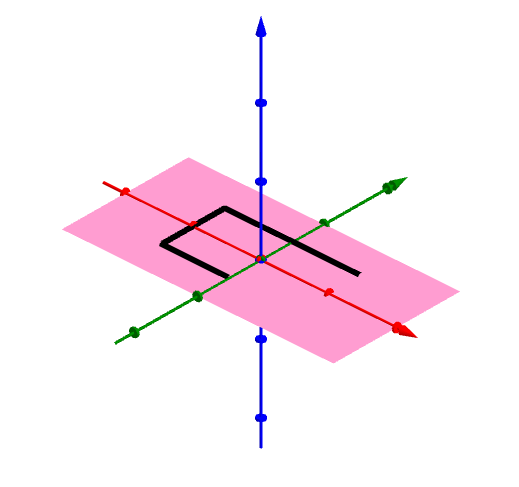
ちなみに、この4操作を3次元空間内での変換と捉えるなら、これらは「なにもしない」「z軸で180°回転」「x軸で180°回転」「y軸で180°回転」と同じことでもあります。

さて、そのような4つの操作について、やはり「2つの操作を連続してやる」という演算を考えると、これも群をなします。

f:id:motcho:20200421101445p:plain

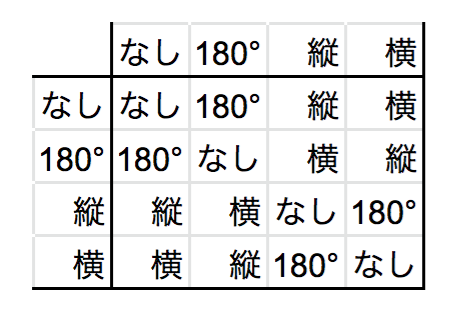
表からわかることとして、「縦方向に裏返してから横方向に裏返すと、180°回転させたのと同じことになる」というのがちょっと非自明で面白いですね。身の回りの物体で確かめてみるといいでしょう。リモコンとか。

f:id:motcho:20200421103458g:plain

𝔽₄の加法群

これはちょっとだけ難しい例なので読み飛ばしても構いません。

2つの方程式「 $\omega^{3}-1=0$ 」と「 $\omega^{2}+\omega+1=0$ 」を満たすような謎の数「 $\omega$ （オメガ）」を考えます。

$\omega^{3}-1=0$ は因数分解すると $\left(\omega-1\right)\left(\omega^{2}+\omega+1\right)=0$ となるため、この2つの方程式を満たす数とはすなわち「3乗すると1になる数のうち、1でないもの」ということを表しています。

これはなにも「この方程式を解け」と言っているわけじゃなくて、「 $\omega$ という数にはこういう関係式が成り立つよ」というだけのことを言っているものだと捉えてください。つまり $\omega$ という数は、3乗すると1になるし、2乗と1乗と0乗を全部足すと0になるようなそんな数だよ（それ以上のことは今は考えないよ）、ということです。

そしていま「 $0,1,\omega,\omega^2$ 」という4つの数を持ってきて、これらに対して「足して、係数をmod2する」という演算を考えます。

例えば、 $\omega$ どうしを足すと $2\omega$ ですが、係数「2」に対してmod2をとると $0\omega$ となり、結局それは0です。

また別の例として「 $\omega^2 + 1$ 」は $\omega$ になります。これは普通に計算すると関係式より $-\omega$ ですが、これの係数である-1に対してmod2をとると1になるので、 $1\times\omega$ で結局 $\omega$ となる、というわけです。

これらの関係性を表にすると以下のようになります。

f:id:motcho:20200421112920p:plain

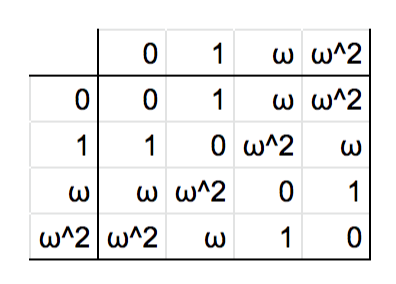
さて、では満を持してこれらの表を比べてみましょう。

f:id:motcho:20200421113231p:plain

ううむ。たまりませんな。完全に一致しています。「旗揚げゲーム」「長方形の合同変換」「オメガの足し算」の間にまったく同じ構造が潜んでいたというわけです。

そして前回出てきた $C_4$ の表と比べてみると、

f:id:motcho:20200421113915p:plain

あきらかに違う構造を有していることがわかります。すなわち、別の群です。

というわけで、この構造には「クラインの四元群」という名前がついています。

クラインの四元群は身の回りによく現れます。ていうか「on/offスイッチ」みたいなものが2つあれば、それでもう完成です。

「何もしない」「スイッチAを切り替える」「スイッチBを切り替える」「両方切り替える」の4操作が、連続して操作するという演算のもとで、上記のクラインの四元群になります（なので、クラインの四元群は $C2 \times C2$ （読み：シーにとシーにとのちょくせき）と呼ばれたりもします）。

だから例えば、これは友人の見出した例なのですが、「定食に味噌汁をつけるかどうかを変える」「サラダをつけるかどうかを変える」「なにもしない」「両方」とかそんなんでも群です。

「構造」にのみ注目しているので、数学的でないものからも群が見いだせることがある、というわけですね。

例２：巡回群の無限系列

別の例を見てみましょう。こんどは前回取り上げた「 $C_4$ 」を一般化することを考えてみます。

前回は「足し算」「掛け算」「正方形」の例を挙げました。

集合「0,1,2,3」と、演算「足して、4で割ったあまりをとる」。

集合「1,3,7,9」と、演算「かけて、下一桁をとる」。

集合「0°回転、90°回転、180°回転、270°回転」と、演算「回転を連続して施す」。

これらの群としての構造は実は同じだった、という話でした。

さて、このうち「足し算」と「正方形」については簡単に一般化を考えることができます。

例えば「足し算」を5要素に拡張したいとするなら、「0,1,2,3,4」という5つの数の集合の上に「足して、5で割ったあまりをとる」という演算を入れれば、それでもう群になります。名前はもちろん「 $C_5$ （シーご）」。

「正方形」の場合は、これを「正五角形」として、「0°、72°、144°、216°、288°」の回転という操作の集合と「連続して施す」という演算を考えれば、やっぱりこちらも $C_5$ になります。

f:id:motcho:20200421131220p:plain

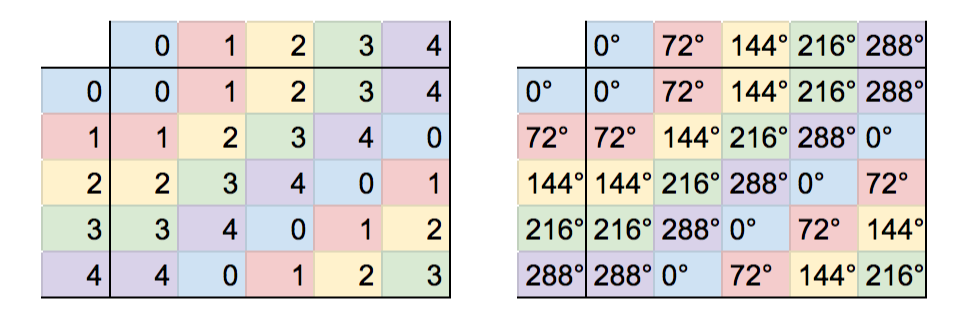
このようにしてできる「巡回群」というタイプの群は実際 $C_6$ 、 $C_7$ 、 $C_8$ …とどんどん増やしていくことができ、自然数の数だけ巡回群が存在します。

「掛け算」の例だけはこのように拡張することが難しくて、あれは実際には「 $(\mathbb{Z}/10\mathbb{Z})^{\times}$ （読み：ゼットオーバーじゅうゼットのじょうほうぐん）」という群なんですが、あのやり方だと $C_6$ は作れますが例えば $C_5$ は作ることができません。

このあたり、ちょっと高度な（だが超面白い）話題です。詳しくは「オイラーのトーシェント関数」なんかでお調べください。

例３：加法群としてのℝ・剪断群

加法群ℝ

群は集合と演算からできていますが、その「もとになった」集合のことを「台集合」といいます。語感がいいですね。

台集合の要素の個数のことを群の「位数」といい、 $C_4$ やクラインの四元群は位数が4の群だということになります。

位数が有限個の群を「有限群」といいます。この記事で前述のものはすべて有限群です。

「有限群」というからには「位数が無限の群」つまり「無限群」というのも存在しているわけです。

「無限」というととっつきにくそうですがなんのことはありません。例えば「実数と足し算」なんかは無限群になります。

実数どうしを足して実数じゃなくなるということはありえないし（閉性）、どの実数と足しても何も変えない「0」があるし（単位元）、どの実数 $r$ にも「 $-r$ 」という、足すと単位元になるような要素があるし（逆元）、結合法則も成り立っています。

4条件を満たしているので、まぎれもなく群です。こういうのを「実数の中で、足し算に注目しているときの群」くらいの意味で「実数の加法群」といいます。

しかも実数は無限個あるので、無限群だというわけです。

剪断群

「行列の集合」の中にも、群になっているものが多くあります。

行列について最低限の知識をインストールしたければ、以下の記事をご利用ください。

www.ajimatics.com

さて、ここで扱うのは $\left(\begin{array}{cc}1 & r \\0 & 1 \end{array}\right)$ という形の行列です。これは図形的には「剪断」を表します。

この行列の右上にある $r$ を増減させながら正方形に作用させると、こんな動きをします。

f:id:motcho:20200421184458g:plain

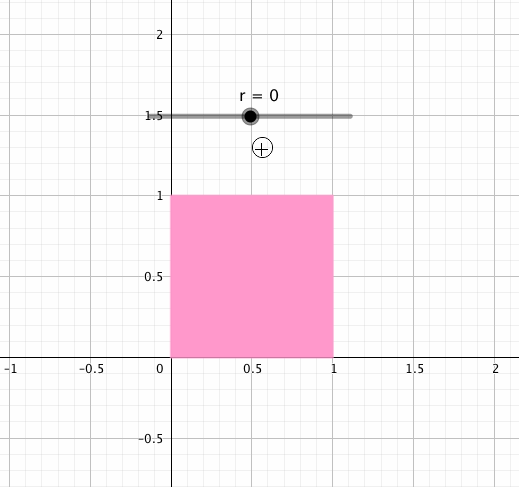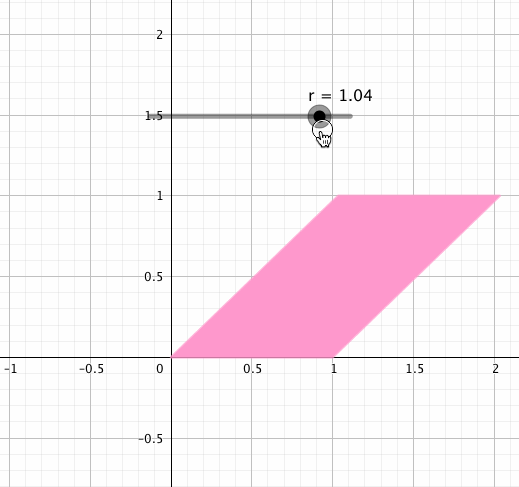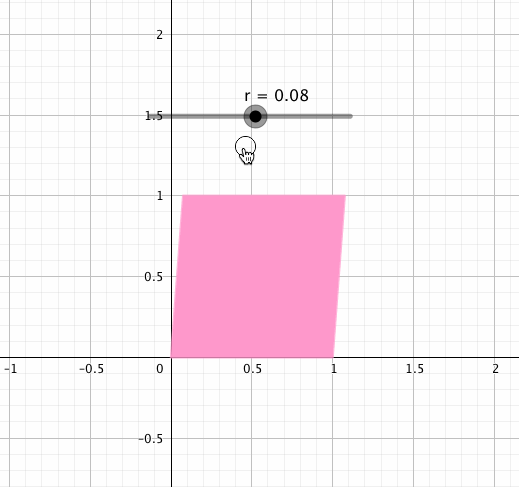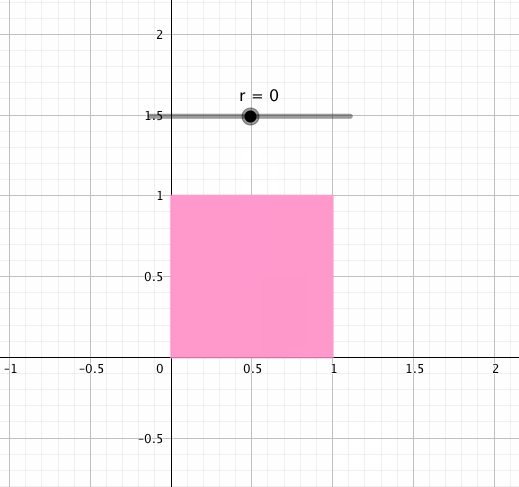
この動きこそが「剪断」です。

で、こういう形をした行列（剪断行列）を全部集めてきた集合は、行列の掛け算に対して群をなします。これを「剪断群」とでも呼んでおきましょう。

この「剪断群」、実はさっき挙げた「実数の足し算」の群と同じなのですよ。

剪断行列2つをかけると、以下のようになります。

　 $\left(\begin{array}{cc}1 & r \\0 & 1 \end{array}\right) \left(\begin{array}{cc}1 & q \\0 & 1 \end{array}\right)$

$=\left(\begin{array}{cc}1 & r+q \\0 & 1 \end{array}\right)$

行列の右上の要素に注目すると、「rとqをかけた結果、r+qになる」ということが起こっています。単純に実数どうしの足し算になったわけです。行列の他の部分は変化していないので、これだけをもって、確かに実数の足し算と同じ構造ということがわかります（非常にラフな言い方）。

これ、なんかよくないですか。「（行列の）掛け算が、ただの足し算と同じになっている」という。

かけたのに、足したことになる。

図形的に見れば、たかが足し算をするためにわざわざ座標をスイスイ動かしているようなものなわけで、その無駄さがなんだかかわいくて好きです。剪断群、私の推し群です。

……余談ですが、数学科の人とかに聞いてみるとこの「推し群」、結構持っている人がいます。

「研究分野なのでブレイド群」

「テストの例を挙げよって問題で挙げたことがあるから自明群」

「人生で何度も感動させられたので $Q_8$ 」

「やっぱ $S_4$ ですかね、学生時代どれだけお世話になったか」

などなど、性格が現れたりして面白いので近くに数学畑の人がいる場合は聞いてみるといいかもしれません。

あるいは、自分なりの推し群を探してみるというのもいいでしょう。

まとめ

ここまで、「クラインの四元群」「巡回群」「実数の加法群」という3つの例を挙げて、いろいろな群を見てきました。

本当はもっと他にも、「3つのものの入れ替えがとある行列群と同じになってるやつ（ $S_3 \cong GL_2 \left( \mathbb{F}_{2}\right)$ ）」とか、「正十二面体の対称変換がいい感じの行列群と一緒になってるやつ（ $I \cong PSL_2 \left( \mathbb{F}_{5}\right)$ ）」とかあって面白いのですが、長くなりすぎるのと前提知識が増えすぎて説明が大変なため、またの機会にしましょう。