ものを知れば知るほど、いつも歩いている道なんかも解像度が上がって見えてくるわけです。
花の名前や雲の種類、建築の様式などはその代表格でしょう。
同じように、知れば知るほど数学の見え方の解像度が上がる(にも関わらず、高校までの数学ではまったくと言っていいほど出てこない)ものの代表格が「線形代数」と「群論」だと思っています。
線形代数については過去にこのブログで扱ったことがあるのでそちらを参照いただくとして、今回は知れば知るほど身の回りにあふれていることがわかって驚かされる「群」という概念のご紹介です。
一体、群とは何なのでしょうか?
とある3つの表
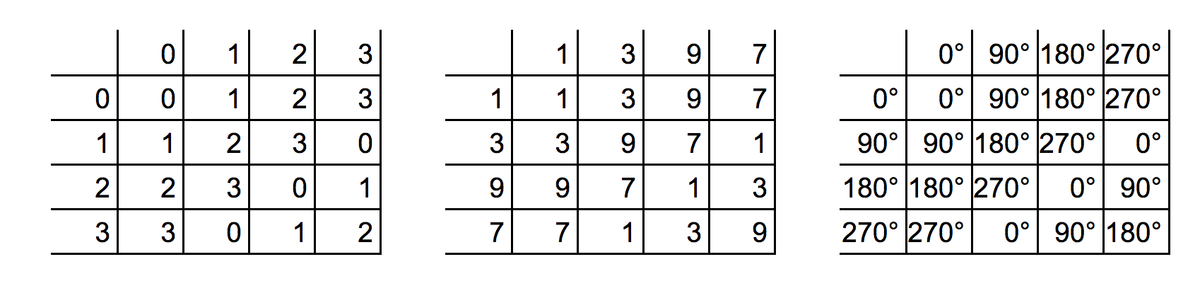
CASE-1 足して4で割る
0,1,2,3という4つの数がありますね。世の中には。
この4つの数に対して、「2数を足して、その答えを4で割ったあまりをとる」という演算を考えます。
例えば「2」と「3」に対してこの演算をすると「1」となります。
2+3=5で、5を4で割ったあまりは1だからですね。
同様に、例えば3と3なら2、2と2なら0、1と3も0、などなど……。となります。
これらのことを表にしたものが以下です。

CASE-2 素数の下一桁
素数というものがあります。この世には。
5より大きい素数は、その下一桁は必ず1,3,7,9のいずれかになっています。
下一桁が偶数だと数自体も偶数になっちゃうし、下一桁が5だと数自体も5の倍数になっちゃうからですね。
さて、この「1,3,7,9」という4つの数に対して、「2数をかけて、その答えの下一桁をとる」という演算を考えます。
例えば「3」と「9」に対してこの演算をすると「7」となります。
3×9=27で、27の下一桁は7だからですね。
同様に、例えば3と7なら1、7と9なら3、9と9だと1、などなど……。となります。
これらのことを表にしたものが以下です。
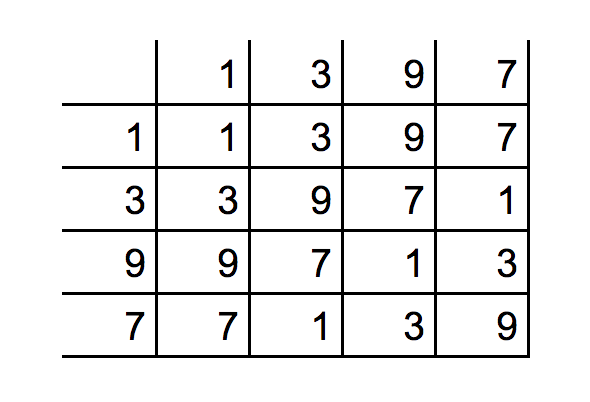
「1,3,9,7」という並びになっているのはいったん気にしないでください。
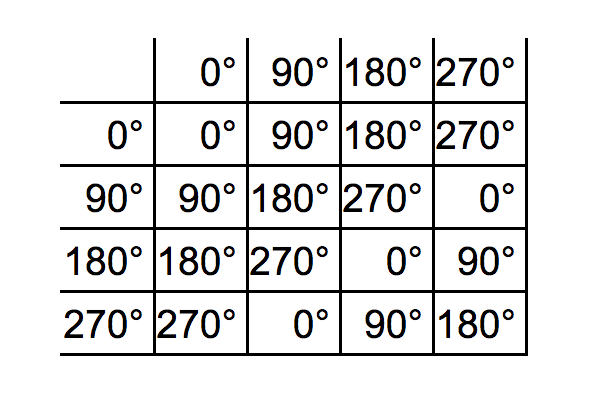
CASE-3 正方形の合同変換
正方形がありますね。世界には。

この正方形に対しての「かたちを変えないような操作」って、どんなものがあるでしょうか。
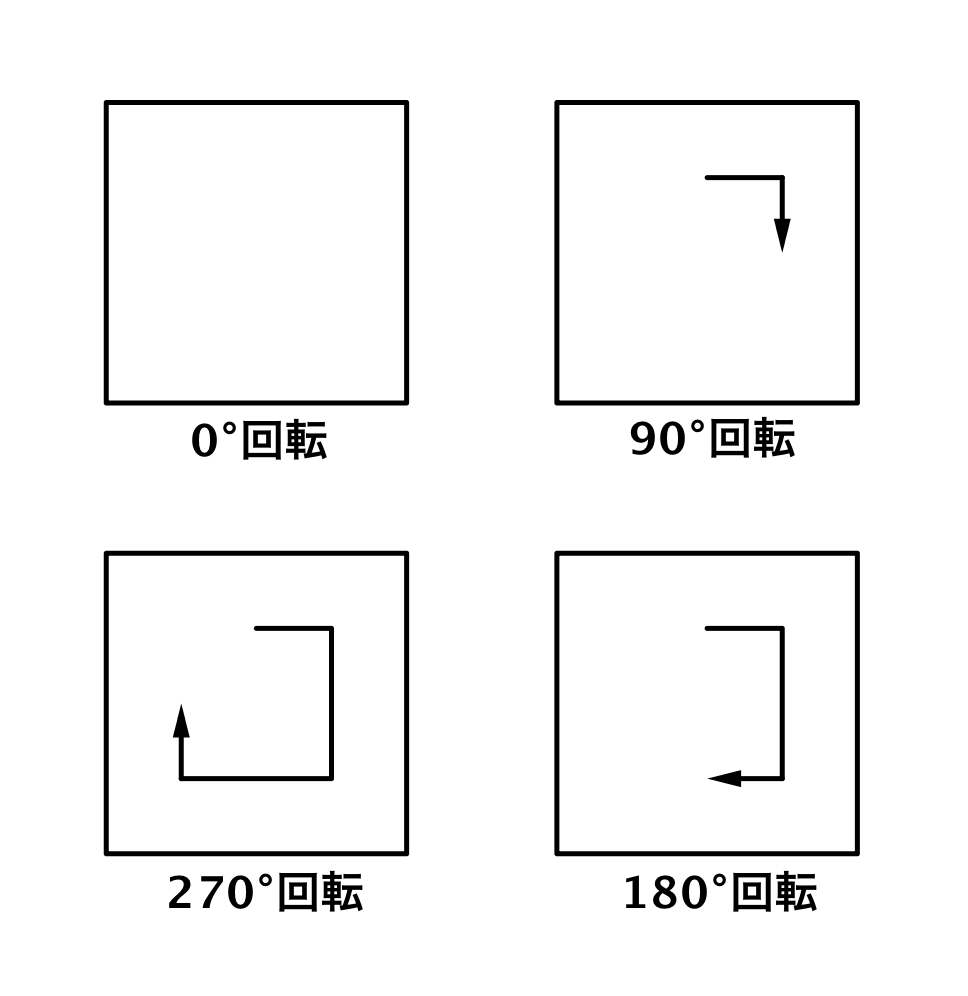
と言われてもよくわからないと思いますが、これは例えば「時計回りに90°回転させる」とかそういうことです。(※この先で出てくる「回転」はすべて時計回りとします。方向は本質的ではなく、どちらでもいい)
正方形を90°回転させても、その操作をする前と後とで「かたち」は変わりません。
「正方形を見てる人が目を閉じてる間にやっても、目を開けたときに気づかれないような操作」と言い換えることもできるでしょう。
かなりお気持ち的な説明ですが。このへんの詳細が知りたい方はより専門性の高い文章をあたってください。
このような操作には「90°回転させる」以外だと例えば「裏返す」などもありえます。が、今回は「裏返す」ということは考えないものとします。
そうすると、正方形に対してのかたちを変えないような操作は4つしかなくて、すなわち「90°回転」「180°回転」「270°回転」そして「回転させない」つまり「0°回転」です。
さてここで、正方形に対してこれらの操作を「連続して施す」ということを考えます。
つまり「90°回転させたあとに、180°回転させる」とかそういうことです。
そして、今あげた例だと実際には270°の回転を施すのと同じことになりますね。
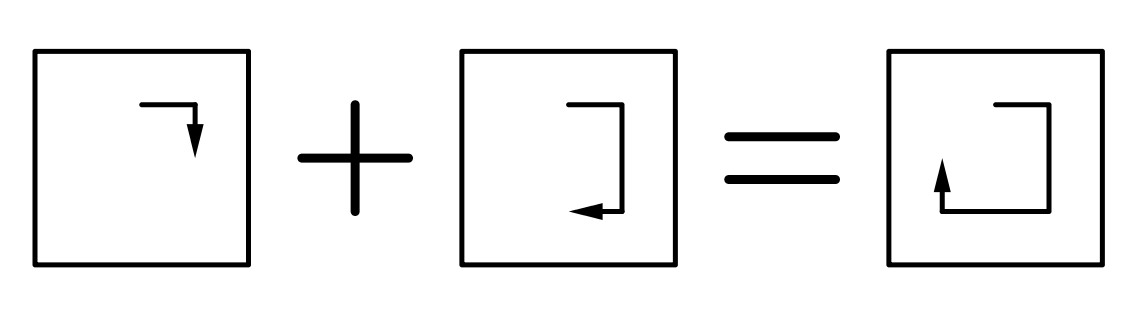
同様に、例えば270°+270°なら180°と同じ、180°+180°なら0°と同じ、90°+270°も0°と同じです。手元に折り紙などを用意してもらって自分で確かめてみるとわかりやすいでしょう。
あとは非常に自明な例ですが、「90°回転を施してから0°回転を施す」というのは90°回転を施すのと同じです。当然ですね。
あるいは逆に「0°回転を施してから90°回転」も90°回転と同じです。至極当然です。
ということで、これら4つの操作の関係性を表にすると以下のようになります。
構造
んん〜〜??
んんん〜〜〜???

まったく同じやないかいかい!!!
ということで、実はこれら3つの表はまったく同じだということがわかりました。
掛け算の表を「1,3,9,7」の並びとしたのはこの「同じさ」をよりわかりやすくするためです。
とはいえじゃあ実際何が同じなのよ?と言われればその「構造」が同じなわけです。
こういう状態はよく「ラベルの張り替えにすぎない」と表現されます。確かに、3つのうちどれか一つの表を持ってきて、そこに書かれている文字ごとに別の文字に書き換えれば、そっくりそのまま別の表になります。
かたや足し算、かたや掛け算、かたや図形の回転と、異なるジャンルのものたちが実は同じ構造を宿していた、というのは、なんとも興味深いものがあると個人的には思います。
そして、同じものには名前をつける価値があるということで、上記のこの構造には「4次の巡回群」あるいは「(シーよん・シーフォー)」という名前がつけられています。
そして言うまでもないかもしれませんが、という構造は群の一種なわけです。
群の詳しい定義は後でやりますが、ここまで出てきた「構造」「群」「」などという語の間の関係性をいったんまとめておくと、以下のようになるでしょう。
・世の中には、今回扱っている数学的な構造以外にもいろいろと「構造」と名のつくものがある(それはそう)。
・その数ある「構造」の中でも一部のものに「群」という名前がついている。
・そして、その「群」という構造の中でも特に、「素数の下一桁」や「正方形の回転」などに現れる構造が「」である
と。そういう関係性です。

そんな群を扱う学問のことを「群論」といいます。
数学では「数」「かたち」「変換」などいろいろなものを扱いますが、「構造そのものを扱う」という点において群論は特徴的なわけです。
何の構造?
さて、「構造」と言っても、構造を持つには何らかの材料が必要です。「なにもないところに構造だけが存在している」という状態は基本的にはありません。建築の構造は建材によって構成されたものだし、社会の構造は人間や法律などによって構成されたものです。
じゃあ「群」という構造は何でできているかというと、「集合」と「(二項)演算」です。
「集合」とは単純に言ってものの集まりのことです。前述の例で言うなら「1,3,7,9」とか。これは数の集まりですね。
「0°回転、90°回転、180°回転、270°回転」というのも集合です。これは操作の集まりですね。
これらの「ものの集まり」があるだけでは群という構造をなしえません。この上に「演算」があってはじめて群になりえるわけです。
で、「(二項)演算」とは、単純に言って「2つのものから新たな1つのものを得る規則」です。あるいは、「その規則を使って実際に新たなものを得ること」という意味でも使います。
足し算や掛け算はその最も馴染み深い例です。どちらも、2つの数を1つの数にすることと捉えられます。
前述のの例だと、「回転を連続して施す」や「かけて下一桁をとる」などが演算にあたります。
この「集合」と「演算」が揃ってはじめて、群になりうるというわけです。
「群は集合と演算との組に対して定義される」という言い方がより正確かもしれません。
なので、集合は同じでも演算が違えば別の群、あるいは群にならない、ということも大いにありえます。
群の定義
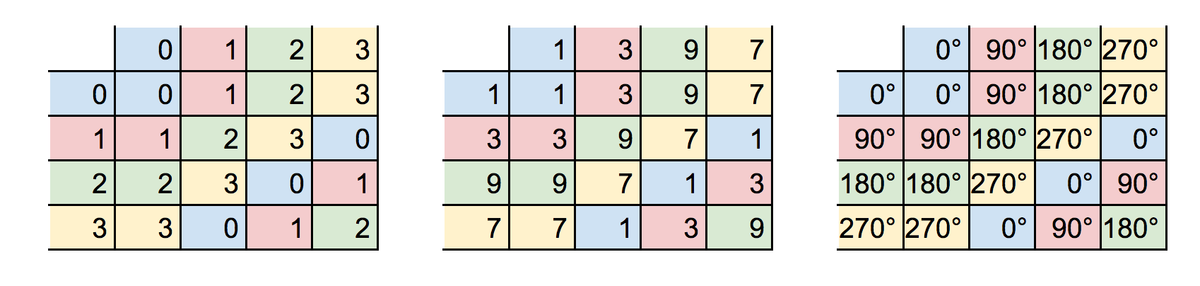
の表を今一度、注意深く観察してみます。なにか気づくことはあるでしょうか(自由記述式)。
・閉性
まずどの表も「はみ出ていない」ことがわかります。あ、いや、書き方とかの話じゃなくて。
「はみ出ない」とは、「どの2つの要素を演算しても、その結果は元の集合に含まれている要素になる」ということです。
この性質を「閉じている」といい、「閉じているかどうか」を「閉性」といいます。まんまですね。これも「集合」と「演算」に対して定義される概念です。
よくわからないでしょうか。つまりはこういうことです。
正方形の回転の例で言うなら、例えば90°回転や270°回転などを何度か連続して施しても、急にその結果が45°回転になったりすることはありません。
0°、90°、180°、270°の回転は、何度施しても必ずまた0°、90°、180°、270°の回転のうちどれかになる。これが、「閉じている」ということの意味です。
掛け算の例でも同じです。1,3,7,9をかけて下一桁をとったら、その結果が5になったり8になったりすることはない。必ず1,3,7,9という集合からはみ出ない。「閉じて」います。
他にも、少し身近な例で言うなら、たとえば「自然数」という集合と「足し算」という演算は、閉じています。
自然数とは、1,2,3,4...みたいな数のことで、マイナスもつかない、小数点もつかないやつらです。(※.000...や.999...は考えない)
どの自然数どうしを足し算しても、その結果も自然数になりますよね。自然数どうしを足し算してるのに急にマイナスや小数点以下の値が生えるということはありえません。
このようなことをもって「自然数は足し算について閉じている」などという言い方をします。
逆に「自然数」という集合と「引き算」という演算で考えると、これは閉じていません。
演算する自然数の選び方によっては、その結果が自然数でないところにはみ出してしまうことがあります。つまり、マイナスがついちゃうことがある。
「自然数は引き算について閉じていない」わけです。(※「開いている」という言い方はあまりしません)
前述の通り、閉性も集合と演算に対して定義されるため、演算が変われば閉じているかどうかも変わる、ということなんですね。
・単位元
ほかにも共通点はあるでしょうか。例えば次のようなものもあります。
どの表の中にも、必ず「どの要素と演算しても、結果を変えない」ような要素があることに気づいた人がいるかもしれません。
それはすなわち「足し算」では0のことであり、「掛け算」では1のこと、「正方形の回転」では0°回転のことを指します。
これらの要素は、いわば「演算しても何も起こらない」要素なわけです。
このような要素のことを「単位元」といいます。
単位元はしかも各表の中にそれぞれただ一つだけ存在するようです。
・逆元
どの表の、どの要素にも、それぞれに「演算すると単位元になるような要素」があることもわかります。
「正方形」の例だと、90°回転に対しては270°回転、180°回転に対しては180°回転(自分自身)、270°回転に対しては90°回転、0°回転に対しては、もちろん0°回転そのものが、それぞれの要素に対して「演算すると単位元になるような要素」です。
このような要素を「逆元」といいます。
逆元は、要素ごとに異なるらしいことも見てわかります。
・結合法則
ちょっと確かめるのは面倒ですが、実はどの表も「どこから先に計算しても結果は同じ」という性質を持っています。
どういうことかと言えば、例えば「掛け算」の表において「3」と「7」と「9」を演算しようと思ったら、
( (3と7)と9 ) のように、「3と7」から先に演算して、その後で9との演算をしても、
( 3と(7と9) ) のように、「7と9」から先に演算して、その後で3との演算をしても結果は同じ、ということです。
「かけて、下一桁をとる」という演算規則に注意しつつ、確かめてみましょう。
( (3と7)と9 )→(1と9)→9
( 3と(7と9) )→(3と3)→9
確かに両方9で同じ結果となりました。
これがどの組み合わせに対しても成り立っていることをもって「結合的である」あるいは「結合法則を満たす」といいます。
3つの表を眺めることで、
・閉じている
・単位元がある
・それぞれの要素に逆元がある
・結合法則を満たす
という4つの共通点を見出すことができました。実はこの4条件が、群の定義そのものなのです。言い換えれば、このような条件を満たす集合と演算こそが、すなわち群です。
これが今回の結論の一つです。解像度の低い順に、「群」とは以下のようなものだったといえます。
・数学的な構造の一種
・集合と演算の構造の一種
・集合と演算の組であって、上記の定義を満たすもの
なんとなく、「群」というものの輪郭がつかめたでしょうか。
いったんまとめ
ここまで、群とはなにか、ということについて見てきました。
それは、もっとも大掴みに言えば「構造の一種」ということでした。
群論では、もともとは何らかの材料を使ってできていた構造に対して、「もともと何から作られていたか」をいわば「忘れて」、構造だけについて調べる、ということをします。
そうすることで、ある構造についての定理なり何らかの結果が得られたとき、「もともと何からできた構造であったか」に関わらず、すべての同じ構造を持つものにその定理を適用できる、などのメリットを得ることができます。
この「抽象化」こそが、数学の重要な仕事の一つではないかと思うのです。
もともとは現実の概念から生まれたものかもしれないけれども、いったん抽象化することにより現実から離れてより深くまで進んでいける。
例えば「累乗」なんかも、もともとは「掛け算の繰り返し」のことだったけれども、それを抽象化することにより負の数乗、分数乗、複素数乗などと進んでいけたわけです。
これは、「数式を現実の事象と結びつける」ということにとらわれ続けていてはできない、かけがえのない営みです。
「群」というのはその中でも特に抽象度が高く、それゆえに応用範囲の広い概念です。
ここまでではその具体例をしか紹介できなかったので、ここから先はもっとたくさんの群の具体例を紹介するつもりでしたが、長くなってきたのでいったんここで切っておきましょう。
次の記事では、「アレとコレとが実は同じ構造」という部分に注目して、数学界にあふれるさまざまな群を紹介していけたらと思います。うひょー! 楽しみ!(自分が)
それでは今回はこのへんで!
