数学的な内容を表現したアニメーションをいろいろ作って遊んでます。例えばこんなのとか。
素因数ビジュアライズ。大きく灰色で表示された数字の素因数が線を横切ります pic.twitter.com/z1MHJzPtbv
— 鯵坂もっちょ🐟 (@motcho_tw) February 7, 2018
たくさんの点を、それぞれの点に書かれた数に応じた速度で回すことにより、大きく灰色で表示された数の素因数を表現しているわけです。楽しいですね。
こんなのもあります。
3Dで図示してみました。 pic.twitter.com/AF2R1QEtqk
— 鯵坂もっちょ🐟 (@motcho_tw) April 12, 2017
九九におけるの段の「一の位」は、ぐるぐる回る点によって表現することができます。面白いですね。
変わったものでは、こういうのもあります。
惑星が「惑星」と呼ばれる理由ですhttps://t.co/2tNtQGJMwb pic.twitter.com/jNYSCDjm2F
— 鯵坂もっちょ🐟 (@motcho_tw) February 25, 2016
オレンジが太陽、青が地球、赤が火星ということで、ある惑星から公転周期の異なる別の惑星を見たとき、夜空を「戻って」見えることの視覚化になっています。興味深いですね。
点を回す
それぞれの動画を解説するのも楽しそうですが、それはまた別の機会にしましょう。
ここまでいろいろなアニメーションを見てきてわかることがあります。どうやらこういうアニメーションを作るにあたっての基本のキは「点を回すこと」のようですね。これまで挙げた動画三つとも、点が回っています。点を回すことができさえすれば、かなりのことができそうだと思いませんか? ですよね。ありがとうございます。
ところが、ここで問題が発生するわけですよ。みなさん、点を回せますか?
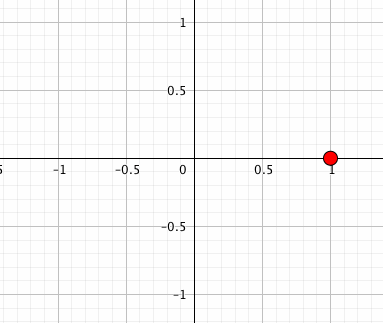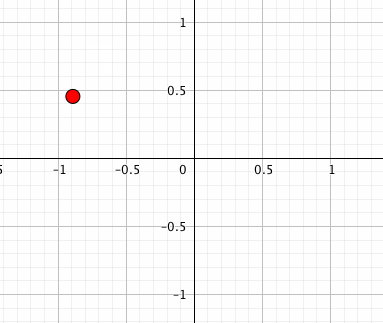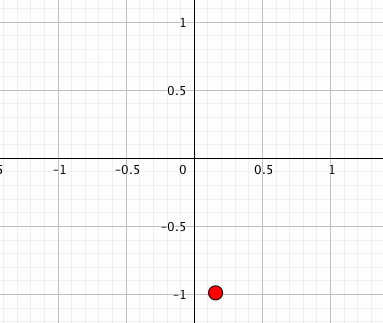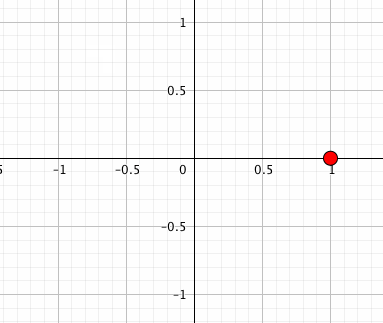
点を回す
なにか描画ツールをはいどうぞっつって渡されたときに、いきなり点を回してのける人ってそんなに多くはないと思うんですよね。
個々の描画ツールの操作方法とかそういう話ではなくて、概念としての話です。つまり、点をクルッと一周回すにはどういうことをすればいいか理解している人は多くないだろう、ということ。
例えば点を一つ描くのは簡単です。座標を指定すればいいのです。、
の位置に点を表示したければ、
と。
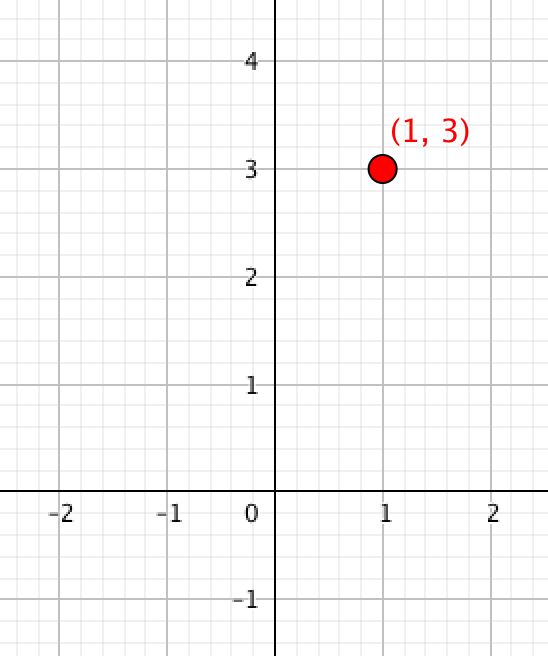
点の指定はという形式で書かれるのが普通ですからね。これで点が描けます。
さてここで、0から1まで動く変数を用意します。「」とでも名付けておきましょう。

そして「」という点を描いてみると、どうなるでしょうか?
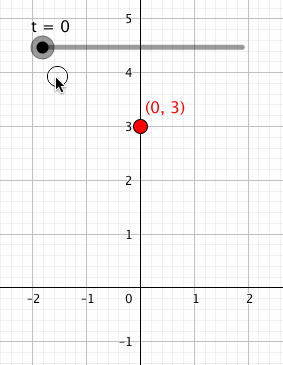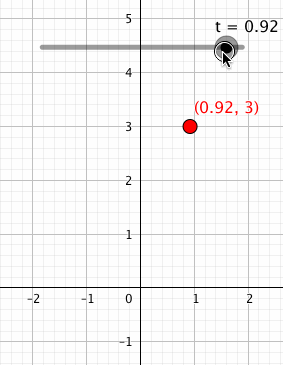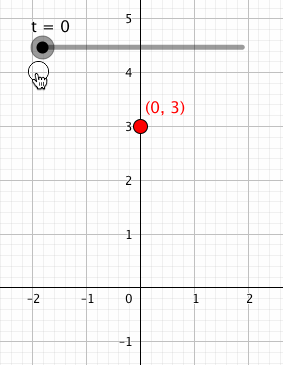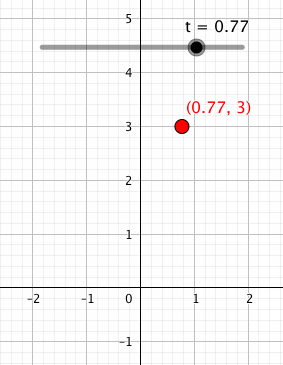
こうですね。が0から1まで動くので、
座標の値は3に保ったまま、
座標の値が0から1まで動く点を描くことができます。
タテに動かしたければとでも書けばいいでしょう。
と書けば、ナナメに動きます。座標の値の中に
を忍ばせてやることで、いろいろな動き方の指定ができます。
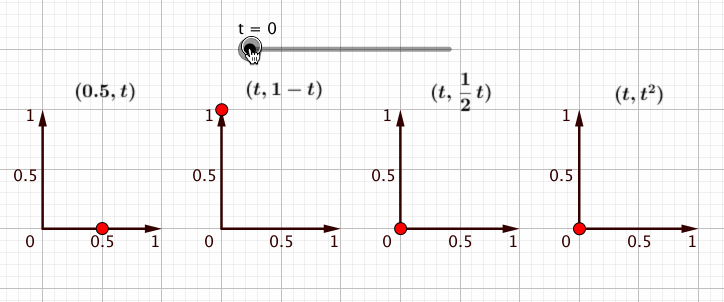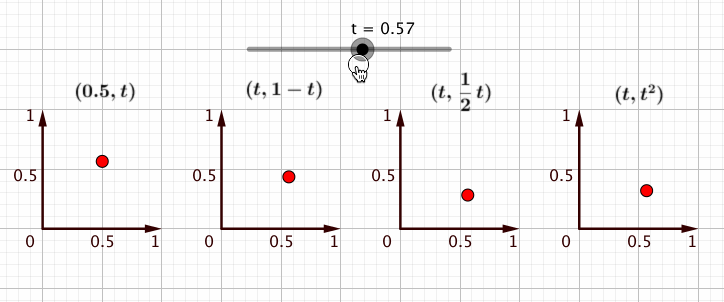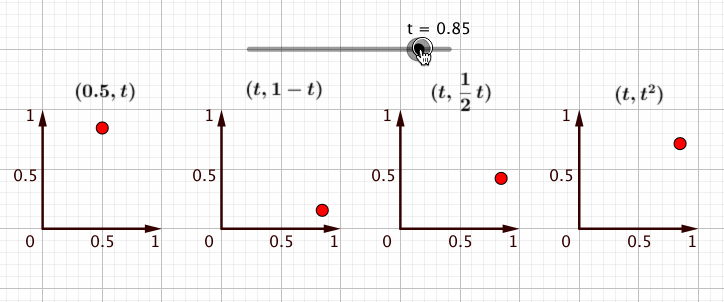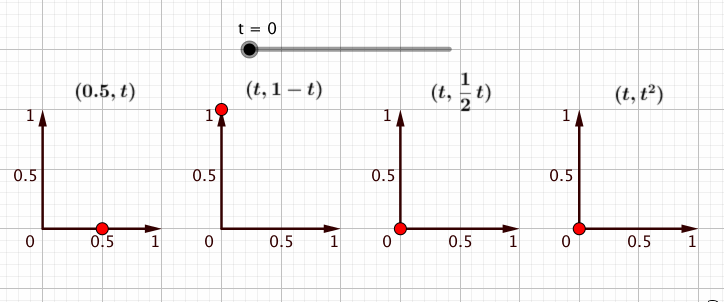
であれば、点を回すにもそのようにすればよさそうだということが察せられてきます。つまり、座標の値にを含んだ点を作って、
を0から1まで動かせばいいのだ、と。
しかし、ここが一番の問題なわけです。点が回ってくれるような座標と
座標の値って?
答えはこれです。ババーン。
こうしておいてを動かせば点はグルっと回ってくれます。出てきましたね。サインとコサイン。「なんの役に立つの?」っていつも槍玉に挙げられるサインとコサインが、実はとっても役に立っていることが判明しました。点を回すのに役立っている。
さて、そうなると気になってくるのは「なぜサインとコサインで回るのか」ってところです。
これは「サイン、コサインというものの定義がそうだから」という答えになるでしょう。
sinとcosの定義
実際のところ、サインコサインとはなんでしょうか。
高校時代、三角関数を学校で習っていた頃、私自身も「とか、
だとかは暗記したから覚えてるけど、じゃあ実際それって何の量を表してるの?」と思ったものです。
これに答えるのは簡単です。これは長さです。と
は、半径1の円(単位円)上で、角度
のところにある点の、
座標の値(横の長さ)と
座標の値(縦の長さ)です。言葉を尽くすと長いですが図で見ると一発です。
と
は、ここの長さのことです。

これは定義です。と
の定義。
「長さ」という直感的な概念なのに「結局何を表してるの?」と思っちゃいがちなのは、おそらく最初はこれらを「三角比」として習うからだと思うんですよね。つまり、直角三角形における「斜辺」と「横の辺」との比が、「斜辺」と「縦の辺」との比が
である、と。
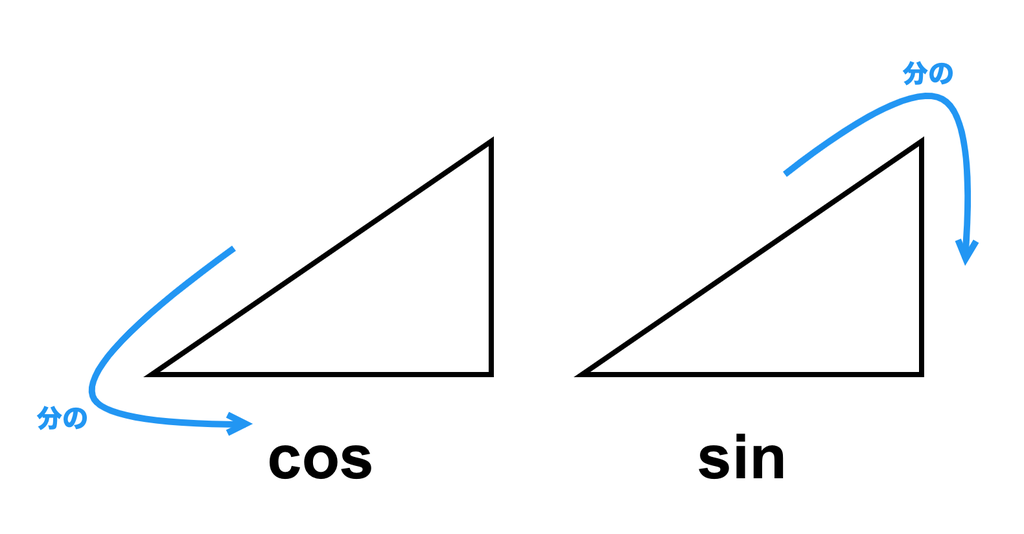
つまり最初はサインとコサインを「長さの比」として習うわけです。だから「結局それってなんの量なの?」ってなっちゃいがち。でも実はこの二つ(「長さの比」と「長さ」)ってほぼ同じことを言っているのです。二つの長さの比って、どっちかを1に固定してしまえば一つの長さになります。
「二つの値の比とは、一方が1のときのもう一方の値である」という言い方もできるでしょう。
直角三角形における「斜辺」と「縦または横の辺」との比は、「斜辺」を1に固定したときの「縦または横の辺」の長さそのものになります。
二つの長さの比だと「結局なんの量なの?」ってなっちゃいがちだけど、一つの長さのことだと言われると「ああ、その部分の長さのことね」ってなってつかみやすいと思います。個人的にはですが。
はい。サインとコサインとがどういう量であるかはわかりました。わかってみれば、これで円が描ける、つまり点を回せることは当たり前に思えます。なぜなら、サインコサインとは「ある角度のときの単位円上の点(の座標)」という定義だったからであり、あとは「ある角度」を0(0周)から2π(1周)まで動かせば勝手に点が回ってくれます。
ということで、さっき作った「」に0から2πまで動いてもらって……。
ん? 「2π」?
2π(にパイ)について
さっきまではを0から1まで動かすって話だったのにここに来て急に0から2πまで動かす話になってしまいました。そのへんの話をしましょう。
角度を表すには「一周の何分の一か」で表すのがよいだろうと人類は考えました。が、その「一周」にどんな数値を充てるかによって、角度の表し方にはいくつか流儀があります。
「度数法」という流儀では一周を360とします。単位は「度」。日常で一番よく使うやつです。しかし実はこの「360」には数学的な意味はあまりありません。せいぜい約数が多いくらいです。
数学的な意味があまりないんだったら別に「360」じゃなくてもいいだろうということで、むしろ一周を「1」とする流儀があってもいいわけです。一周が1だとすると、度数法でいう「90°」は「」に、「210°」は「
」になるでしょう。
でもこの一周を1とする流儀はあまり使われていなくて、数学界で一番よく使われる流儀は、一周を「2π(=6.28...)」とする「弧度法」です。単位は「ラジアン」。文脈が明らかならば単位のラジアンは略されることも多いです。
一周を2πラジアンだとする弧度法には、「角度の値がその角度に対応する単位円の弧の長さと等しくなる」という特徴があります。
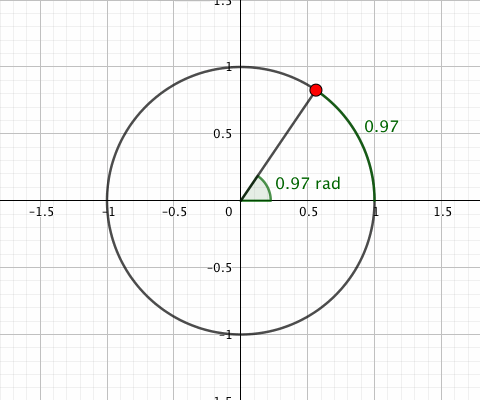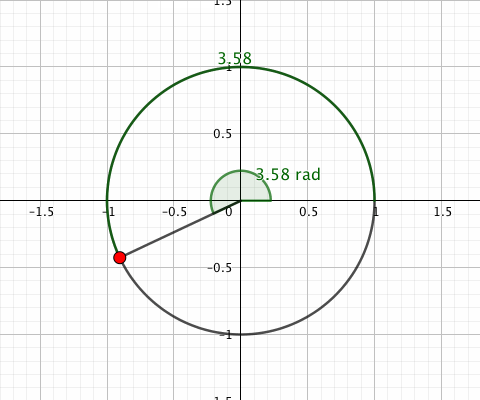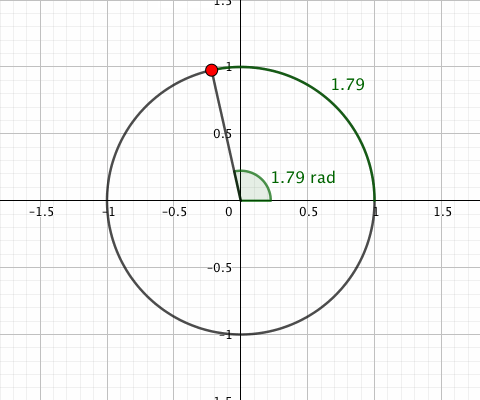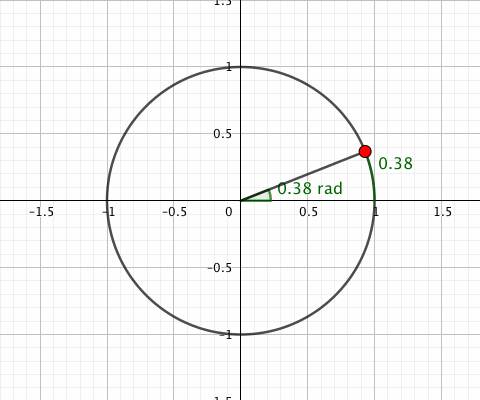
ではなぜ等しくなる値を使うのか。つまり2πという値を使うメリットですが、とりあえず「微分方面でいろいろある」とだけ思っておいてください。いろいろあるんですよ。微分方面で。一周を2πとしてあると微分方面でいろいろ都合がいいんですよ。しかし本題とはそれるためここでは解説しません。
なんにせよ、この記事では、いくつか流儀がある中の弧度法を使って角度を表示しています。それでという点の表示になったわけです。これで
に0から1まで動いてもらえば、サインとコサインの中身は0から2πまで、つまり一周分動くことになります。
そうすれば、という点は一周分グルっと回ってくれる、という寸法です。
点を回せるとできること
点を回せさえすればかなりのことができると申し上げました。ここからは、を出発点にどこまでのことができるのか見ていきましょう。
例えば、ここをこうしてみます。
sinの前に「2」を入れてみたわけです。すると……。
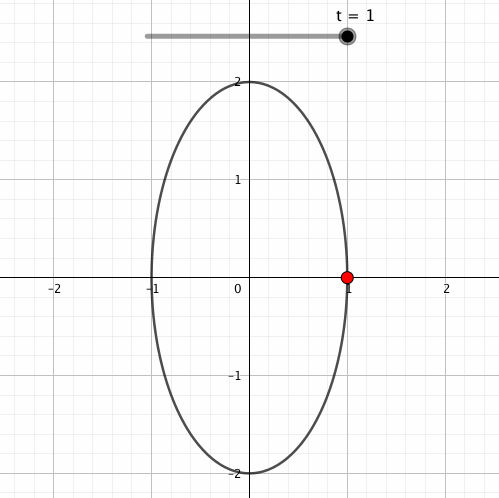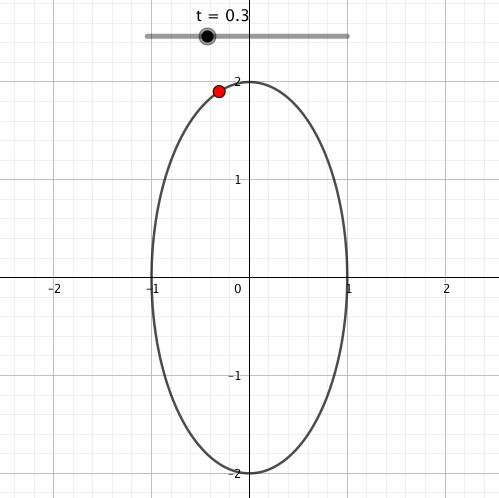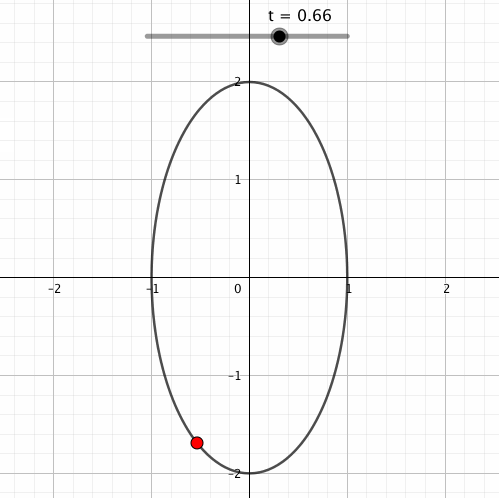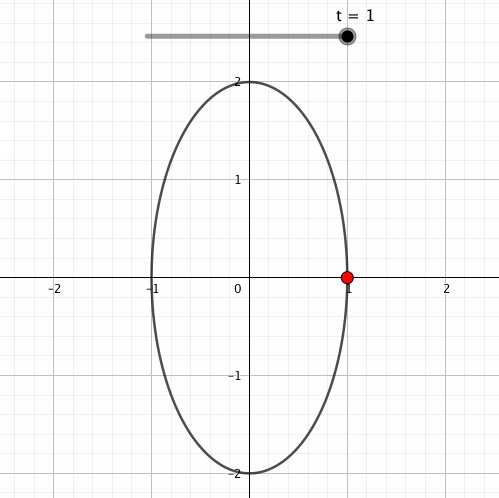
こうなります。上記の数式で描画できるのは赤い点だけなのですが、軌跡も黒の線で表示してみました。
sinやcosの外側にかけられた数は回転の半径に影響します。sinが縦の長さなので縦の長さだけ2倍されている感が出ましたね。
「2」をsinの前につけるとこうなりましたが、こんどはsinの中に入れてみましょう。
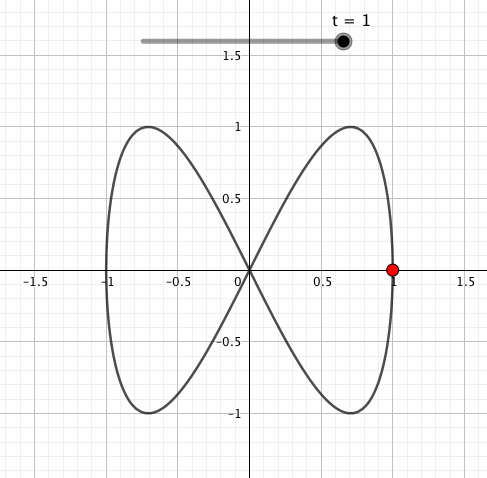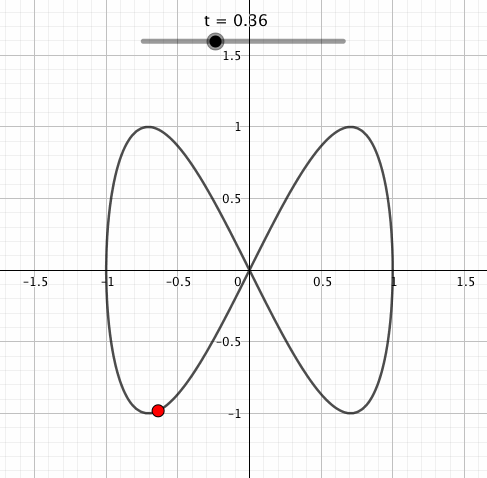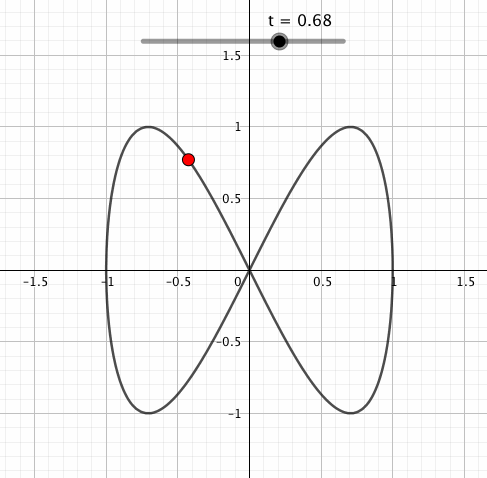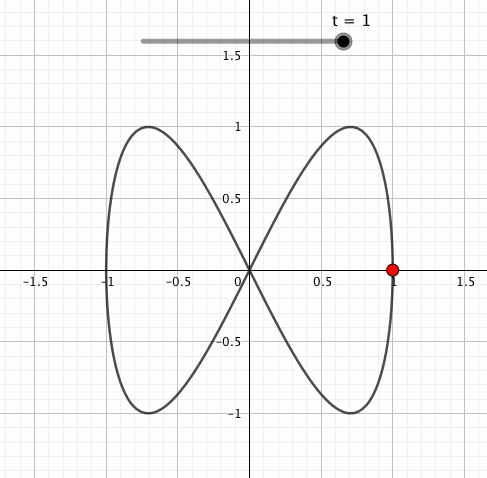
sinやcosの内側にかけられた数は回転数に影響します。cos(横往復)とsin(縦往復)の中身を比べると、sinだけが2倍になっているので「横に1回往復する間に縦に2回往復する」感じになっていることがお分かりいただけますでしょうか。
横を3、縦を5とするとこんな感じになります。

横が3往復してる間に縦が5往復するさまをお楽しみください。こういう単純なサインコサインの軌跡として描かれる図形のことをリサジュー図形といいます。
点を複数設置してみるとエモが増します。例えば中心からの距離が大きいほど回転速度も速くしてみるとこんな感じ。
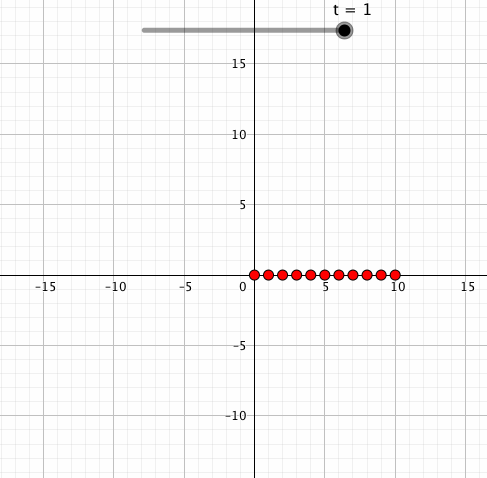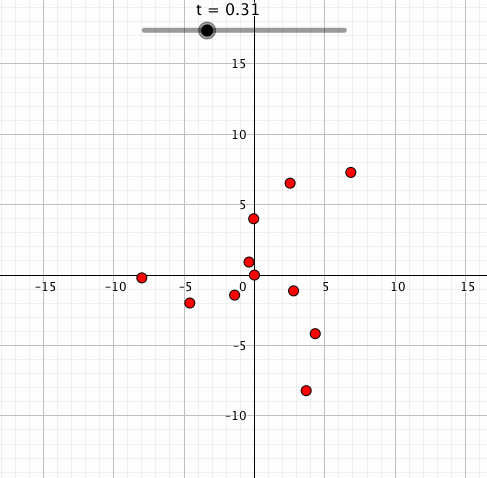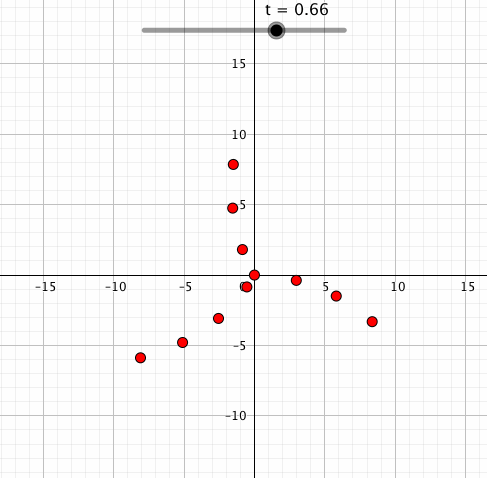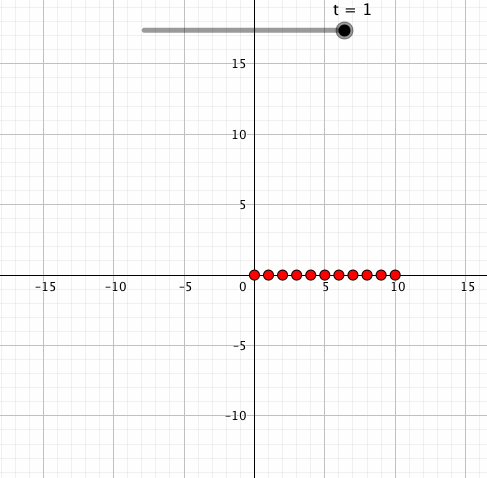
なんかこんな感じのちょっとした小ネタにも使えます。
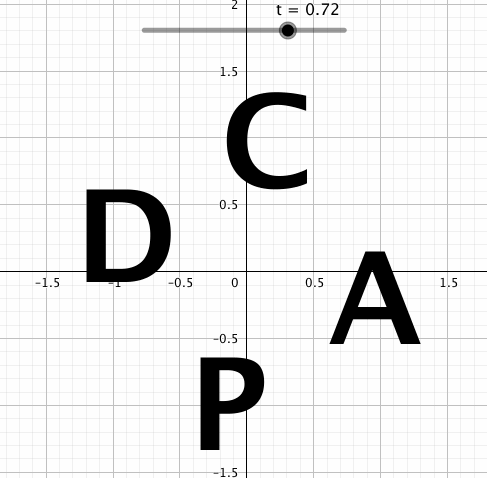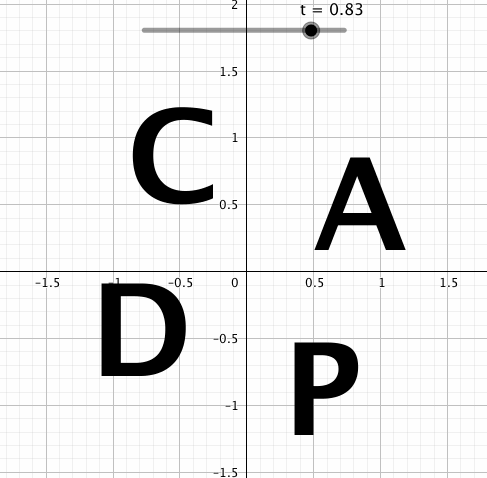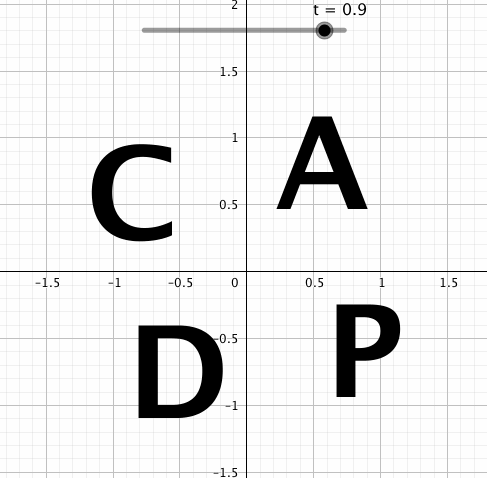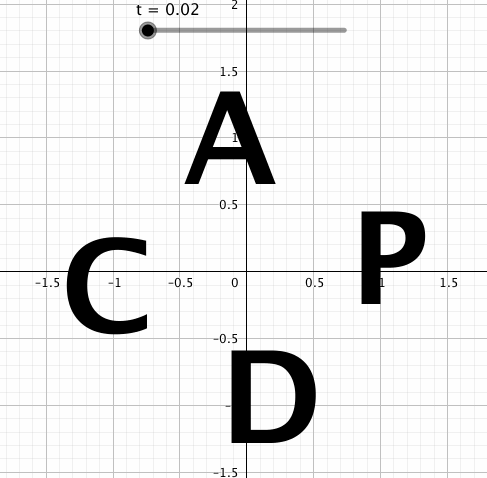
えーとはい。
ぜひ遊んでほしい
回転する点は、少し数式をいじるだけで思いもよらない変化をすることがわかります。実はこれ、ぜひ皆さんにもやってほしいのです。
というわけで、こちらにご用意いたしました。
リンク先には数式の入力欄がありますので、の後の部分をいじってみてください。
さっきみたいに「sinの前に2をつけたらどうなるかな?」とか「2乗してみたらどうなるかな?」みたいなことをいろいろやってみて、このブログのスローガンである「ここをこうするとおもしろい」を是非体感してみていただけると嬉しいです。
三角関数が役に立つのか立たないのか、全員が履修すべきかすべきでないか。私そういう関連のことにはあまり詳しくないのですが、少なくともこうやって楽しく遊ぶことはできます。
普段使う使わない、履修したしないにかかわらず、人類はみな、三角関数で楽しく遊ぶことができます。
それでは今回はこのへんで!

