この記事は、線形代数において重要な「行列式」の概念だけを、予備知識ゼロから最短距離で理解したい人のための都合のいい記事です。
そのため、わかっている人から見れば「大雑把すぎじゃね?」「アレの話するんだったらアレの話もしないとおかしくね?」という部分が少なくないかもですが、趣旨をご理解いただいた上でお付き合いください。明らかな間違いに関しては、ご指摘いただけますと助かります。
線形変換

↑座標です。
座標を変形することを考えます。つまり、座標変換です。
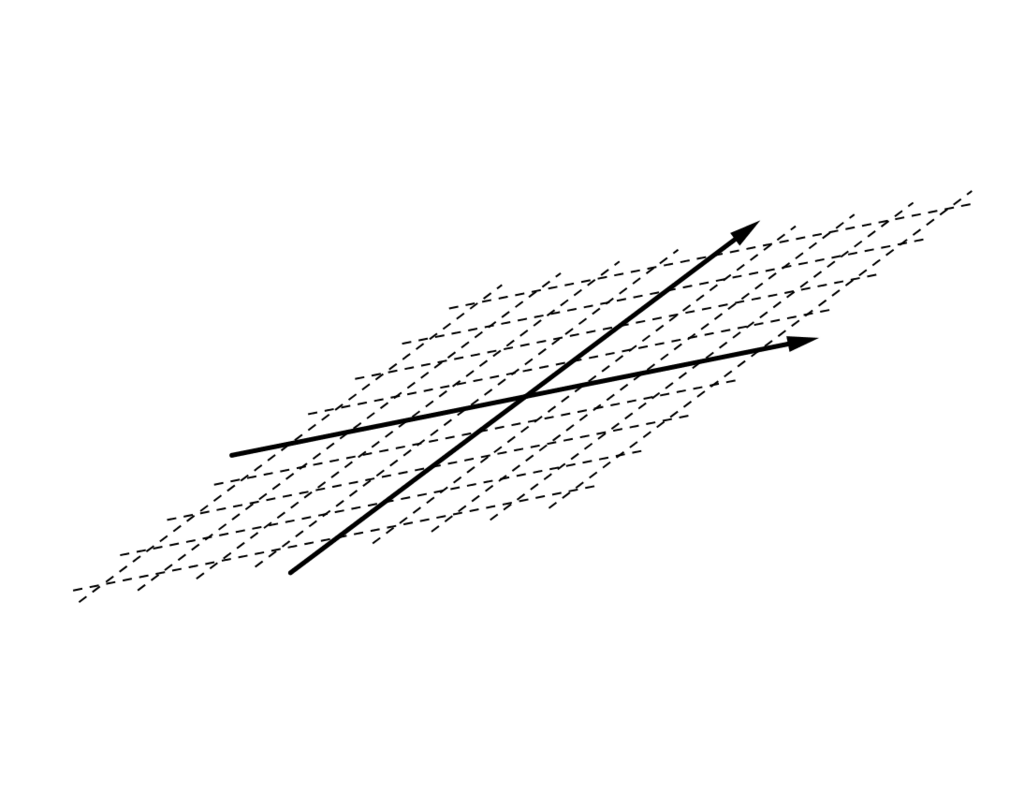
座標変換にもいろいろあって、以下のようにグニュッと曲げたやつ

も座標変換には違いありませんが、今回ここで考えるのは線形変換だけにします。線形変換とは大雑把に言えば「すべての直線を直線に保つ」「原点を動かさない」という条件を満たす変換です。
そういう変換には例として、伸ばしたり縮めたりの拡大・縮小(scale)、原点中心に回す回転(rotate)、原点を通る直線で鏡写しにする鏡映(reflect)、ある方向は保ったまま別の方向を「ずらす」剪断(shear)などがあります。
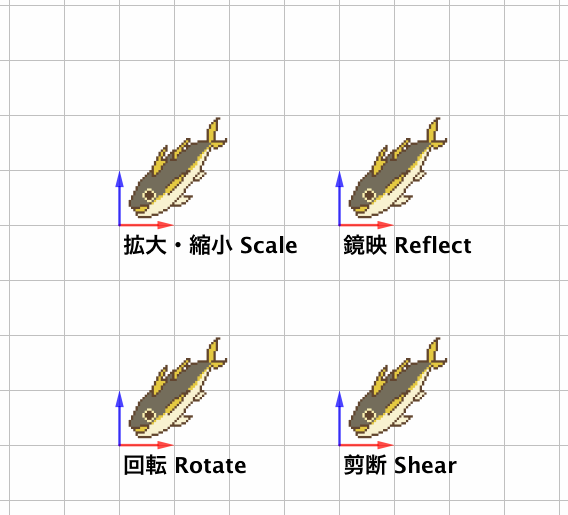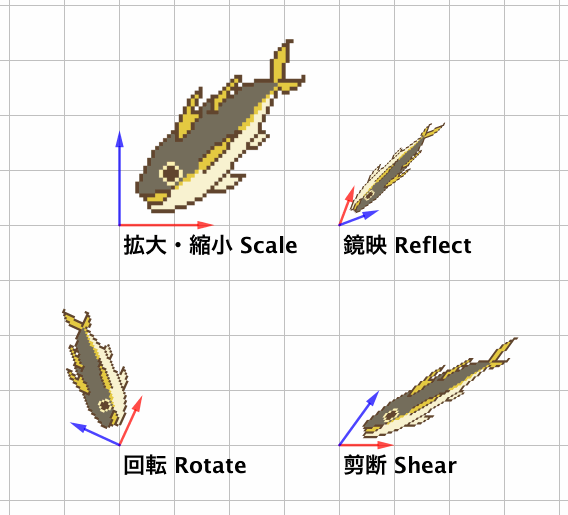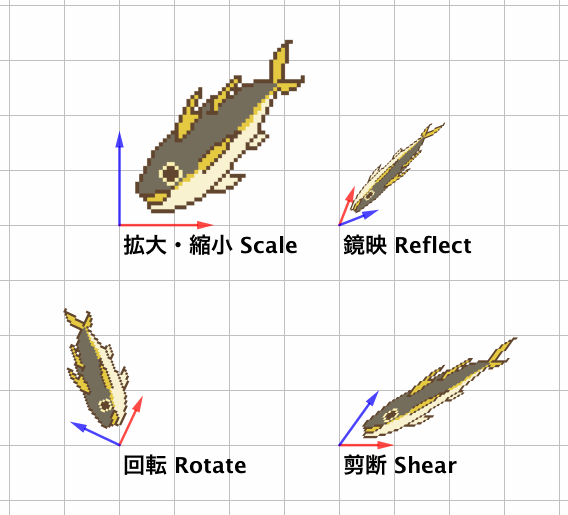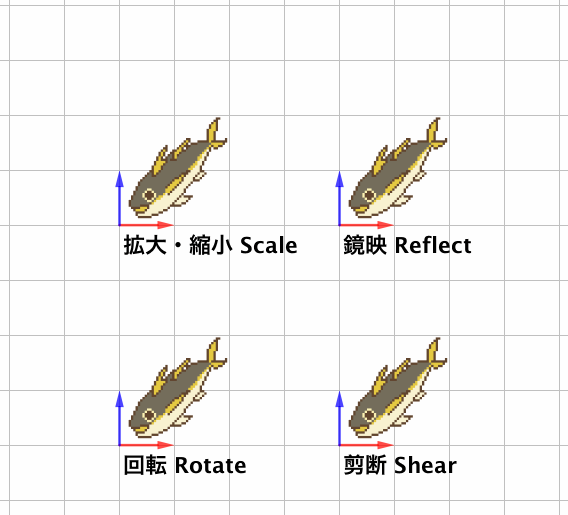
これらはどれも、「すべての直線を直線に保つ」「原点を動かさない」という線形変換の条件を守っています。
さらに、これらを基本にして、例えば「拡大してから、回転」「鏡映してから、剪断」などのように、これらの組み合わせで実現できる変換も、線形変換になります。
対して、「平行移動」「原点以外の点中心での回転」などは、線形変換にはなりません。直線は直線に保つけど、原点が動いちゃうからってことですね。
さて、ここで大事な事をいうので心して聞いてほしいのですが、すべての線形変換は「2つ※のベクトルがどう動くか」という情報「だけ」で表現できます。
※2次元のとき。n次元ならn個。
ベクトル
ベクトルとは、簡単に言えば「座標上に置かれた、原点から出る矢印」のことです。
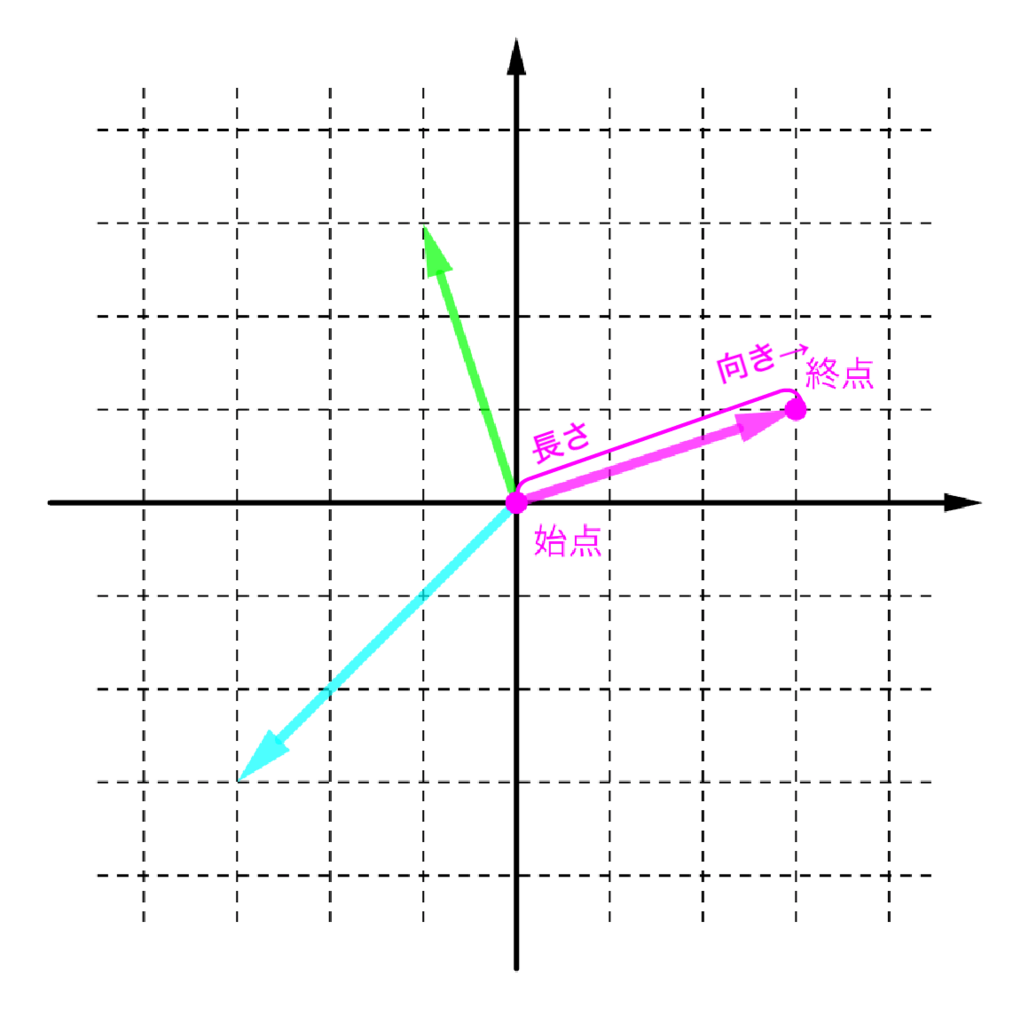
まっすぐな矢印、つまり有向線分には「大きさ(長さ)」「向き」「始点」「終点」などの情報がありうるのですが、ベクトルはそのうちでも始点を原点に限っているものをいいます。なので、すべてのベクトルは「終点がどこにあるか」という情報「だけ」で表現できるということになります。
つまり、任意のベクトル(原点から出る矢印)を一つ指定するには、終点の座標さえ指定すれば事足りる、というわけです。終点さえ決まれば長さも向きも決まるからですね。
ベクトルはふつう、終点のx座標、y座標をタテに並べてと書かれます。
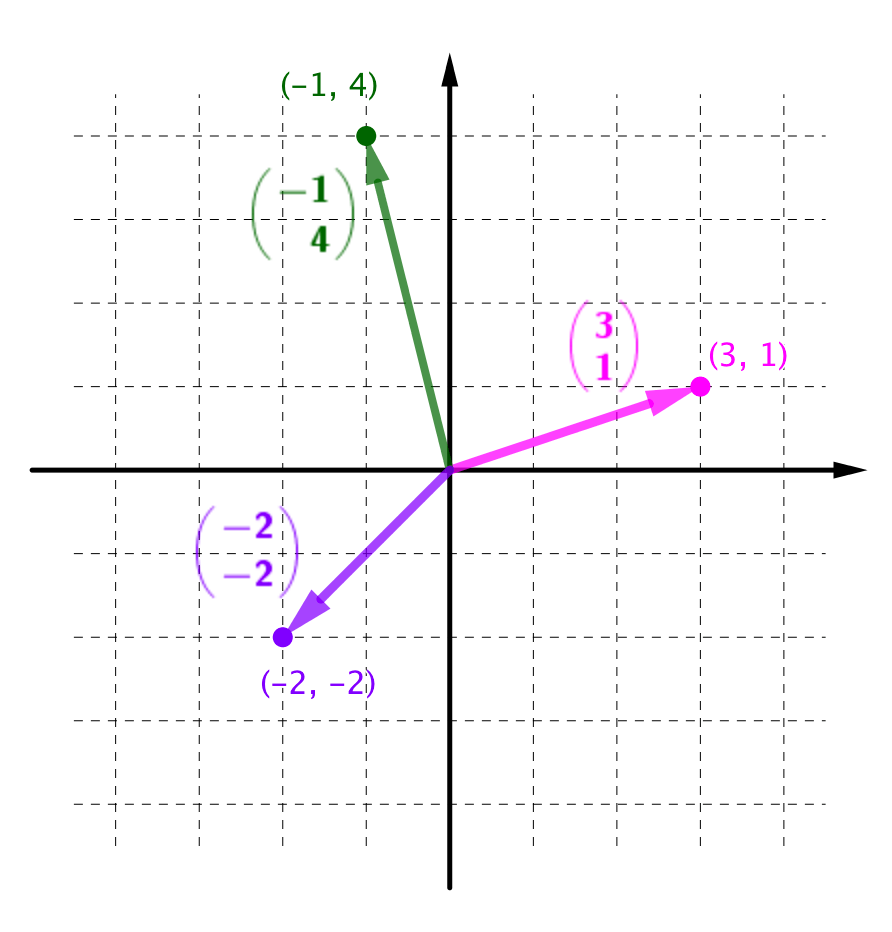
そして、前述の「2つのベクトルがどう動くか」とは要するに「基準となるベクトルを2つ決めて、それらがそれぞれどのベクトルに変化するか」ということを意味しています。
例を見てみましょう。「基準となるベクトル」としてと
を採用します。説明の便宜のため、
に「
」、
に「
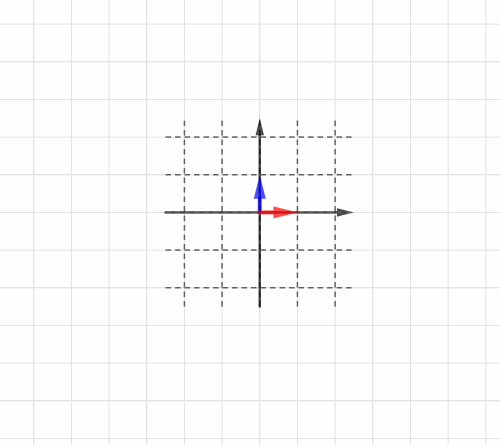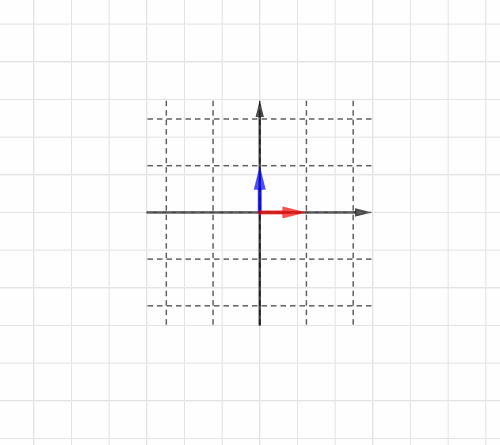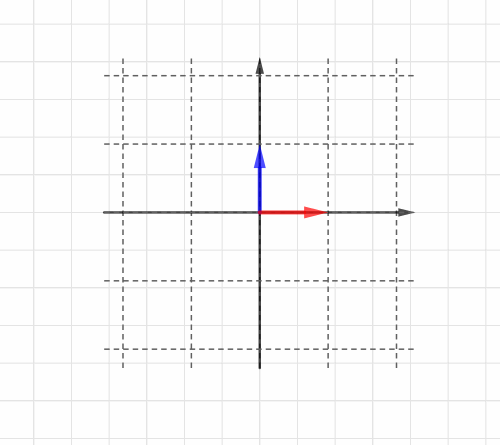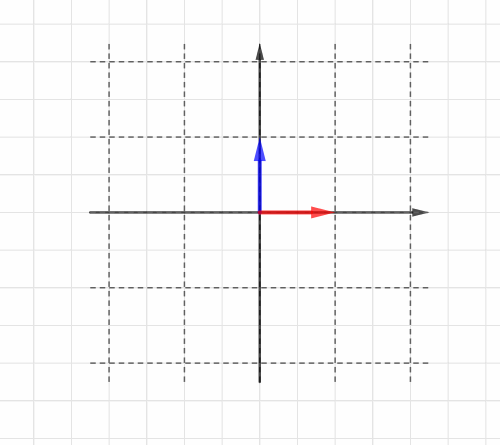
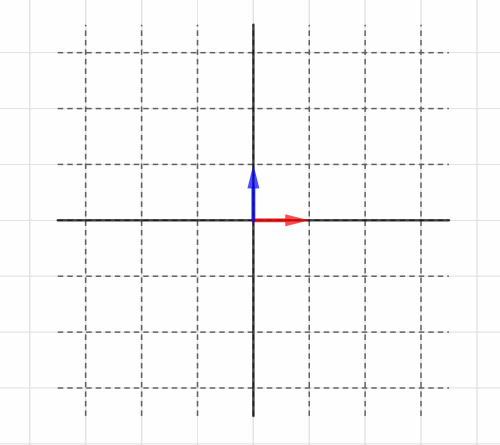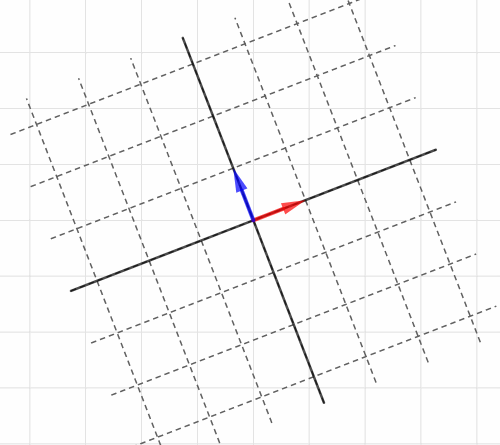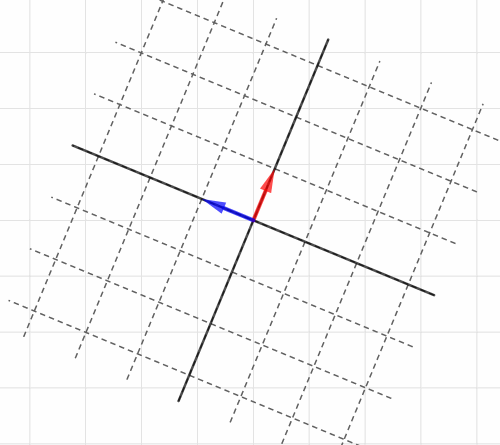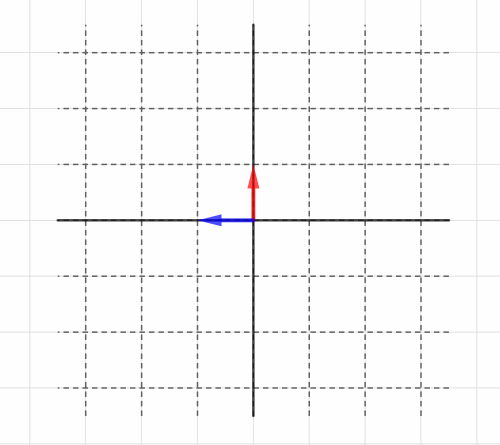
」と名前をつけておきましょう。図に示すとコレです。
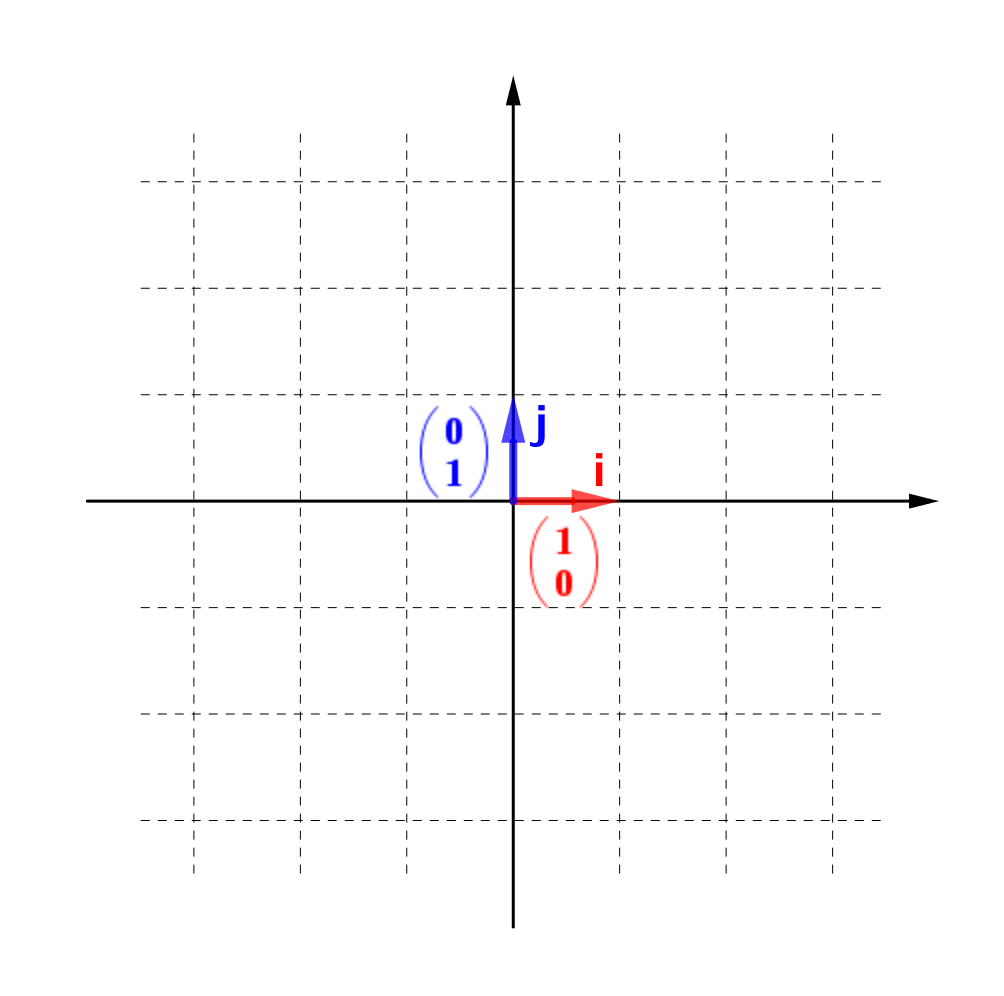
どちらも、終点のx座標とy座標がタテに並んで表現されていますね。
「それらがそれぞれどのベクトルに変化するか」ということですが、ではいまが
、
が
に変化したとしましょう。

この情報だけが、「座標全体が2倍に拡大」という線形変換を表します。
こんどはが
、
が
に変化したとします。
この情報だけが、「座標全体が左に90°回転」という線形変換を表します。
座標上の一つ一つの点について細かい指定をしなくても、と
がどこに動くかさえわかれば、すべての座標上の点がどこに動くかわかるのです。すごい。これは「すべての直線を直線に保つ」「原点を動かさない」という条件があるおかげです。
動かしはじめの基準であると
のことを基底ベクトルといいます。基底ベクトルさえ指定してしまえば、すべての線形変換は、「変化先」のたった2つのベクトルを指定するだけでただ一通りに決まります。
例えば、「座標全体を1/2に縮小」を表したければ「と
」。「3倍に拡大、かつ、x軸に関する鏡映」を表したければ「
と
」、とだけ言えばすむわけです。
さて、いちいち「と
」などと表現するのはめんどくさいので、ここはハイパー便利概念である行列を使ってひとまとめにしましょう。
行列
行列とは、簡単に言えば「タテヨコに要素が並んだもの」のことです。例えばこんな感じ。

数学では、こいつを足したり引いたりかけたりと、それ自体が「数」であるかのような扱いをします。
行列の中に入ってるもの(要素)は四則演算できればだいたい何でもいいですが、上の例では数ですね。
行列のうち、行(ヨコ)と列(タテ)の長さが同じ、つまり正方形に並んでいるものを特に正方行列といいます。また、行や列の長さを「次数」といい、上記の図の左側のものは「3次正方行列」となります。
行列は線形代数で扱われる主要な対象であり、誤解を恐れずに言えば「線形代数」とは「行列の学問」です。
さて、ベクトルを2つ指定するのはめんどくさいという話ですが、行列を使えば複数のベクトルをひとまとめに表現できます。横にくっつけるのです。
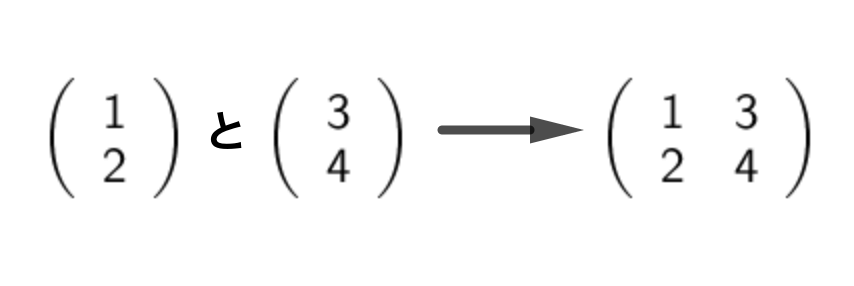
そんだけ。ほんとにそんだけ。このことは、行列の演算方法から正当化されるのですが、今は深入りしません。
つまり、この一つの2次正方行列だけで、2つのベクトルを表していることになります。そして、2つのベクトルで、一つの線形変換を表しているのでした。すなわち、この一つの2次正方行列だけで、一つの線形変換を表している、ということになります。
例えばという行列なら、
を
、
を
に持っていく変換を表す、というふうに。
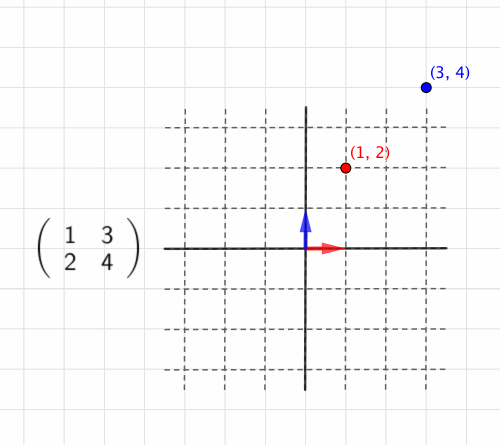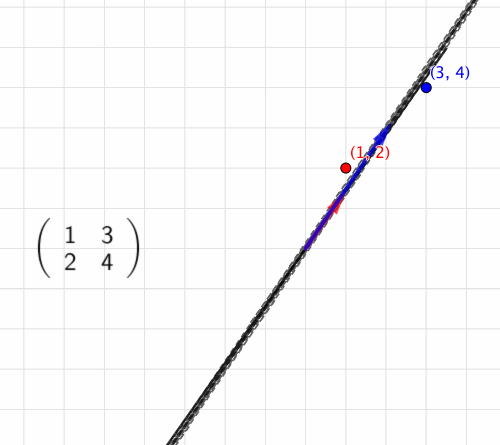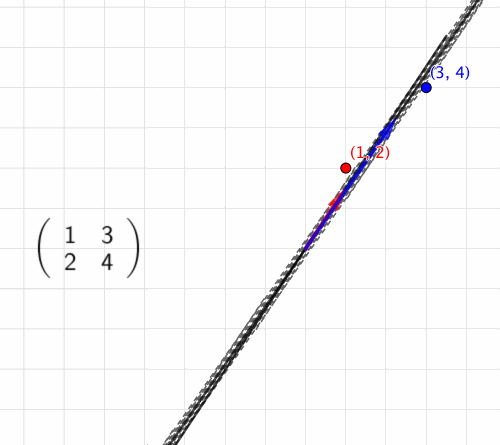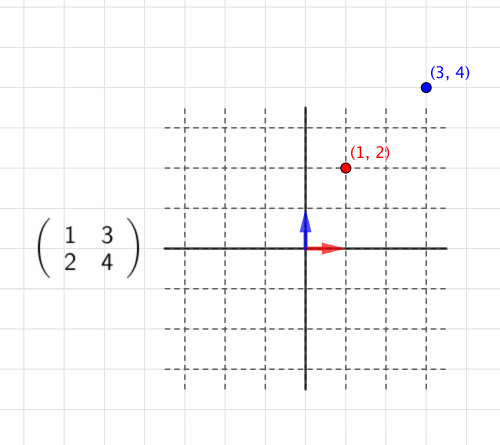
[座標]を[行列]で「変換する」、[座標]に[行列]を「作用させる」などの言い方をします。
行列の本質
冒頭で「最短距離で理解」と言った手前あれなのですが、ここでちょっとだけ脱線させてください。
「行列とは何か」とはよく問われる疑問です。確かに、行列ってなんか数字が並んでいるだけでその演算方法も謎に複雑だし掴みどころのない概念だと思ってしまう気持ちはわかります。行列はいろいろなものを表せるので、行列とは何かと聞かれたら「行列とは行列である、と言うしかない」と答えるのはもちろんそれはそれで一つの答えだし、正しくて誠実だと思います。
さて、ここで私大きな事を言ってしまいたいのですが、
行列とは、線形変換です。
それぞれを相互に読み替えてもいいくらいです。もちろん、連立方程式だったり、グラフの隣接関係だったり、行列は線形変換以外にもいろいろなものを表せることは百も承知の上です。
「行列とは何か」という問いは、「数とは何か」という問いに似ています。「数」という概念なんて行列にも増して、「数とは数である、と言うしかない」ような存在だと思います。しかし、例えば算数を習いはじめの小学生には「数とは個数である」として教えたほうが、その概念を掴みやすく、理解する、という点においては効果的であるはずです。「数って何なの?」という疑問を持つ小学生に対して「数とは数である、というしかない」と答えることは確かに誠実かもしれませんが、理解させる、階段の一段目を登らせるという点においてはあまり万人に対する効果はないでしょう。
それと同じだと思うのです。行列はいろいろなものを表すけれども、とりあえずすべての行列を線形変換の表れだと思ってもらって、それを階段の一段目とする。掴みどころのない概念に相対し続けるよりは、初学者にとってはそのほうがやりやすいと、個人的には思います。
しかも、「行列とは線形変換」は、「数とは個数」よりある意味では正しいのです。「数とは個数」という捉え方のままだと、すぐに対応できない概念が登場してしまいますが(例えば、)、「行列とは線形変換」はむしろそれが行列の本質だと言ってしまっていいくらい、正しい捉え方なのです。やったね。
数学で扱う主なものにはそれこそ「数」「かたち」「式」などがありますが、「行列」を手にしたことによりわれわれは新たに「変換」つまり「動き」を数学的に扱う言葉を手にしたことになります。
行列式
話を戻します。ここまでで、行列一つで一つの線形変換を表すことがわかりました。これは変換する座標の次元が上がっても同じことです。ここまでずっと2次元平面の話でしたが、3次元では3次正方行列がその変換を表し、4次元では4次が……以下同じです。

(3次の座標変換)
さて、ここでこんな事を考えます。一つの線形変換から取り出せる情報にはどのようなものがあるか?
ここに来てようやく、入口にたどり着きました。つまり、その答えの一つが、今回のメインテーマである「行列式」というわけだったんです。つまり行列式とは、一つの線形変換(≒行列)から取り出せる情報の一つである。と。
では、どんな情報か。例えば、その線形変換がどのような変換か、つまり拡大なのか回転なのか鏡映なのか剪断なのかそれらの組み合わせなのか、というのも情報の一つです。回転ならば何度回転なのか、鏡映ならば軸はどこなのか、という情報を取り出すこともできるでしょう。
あるいは、座標を線形変換させたときに、その座標がどれくらい伸び縮みするのかという情報もありえます。つまり、倍率です。こちらは情報の中でも、具体的な数としてでてくるはずです。
これを考えるのは、実はそんなに難しくありません。座標の中の一つの「格子」に注目すればいいのです。
変換される前の座標の中の、の4つの点で描かれる正方形を考えます。もちろんこのこいつの面積は1です。
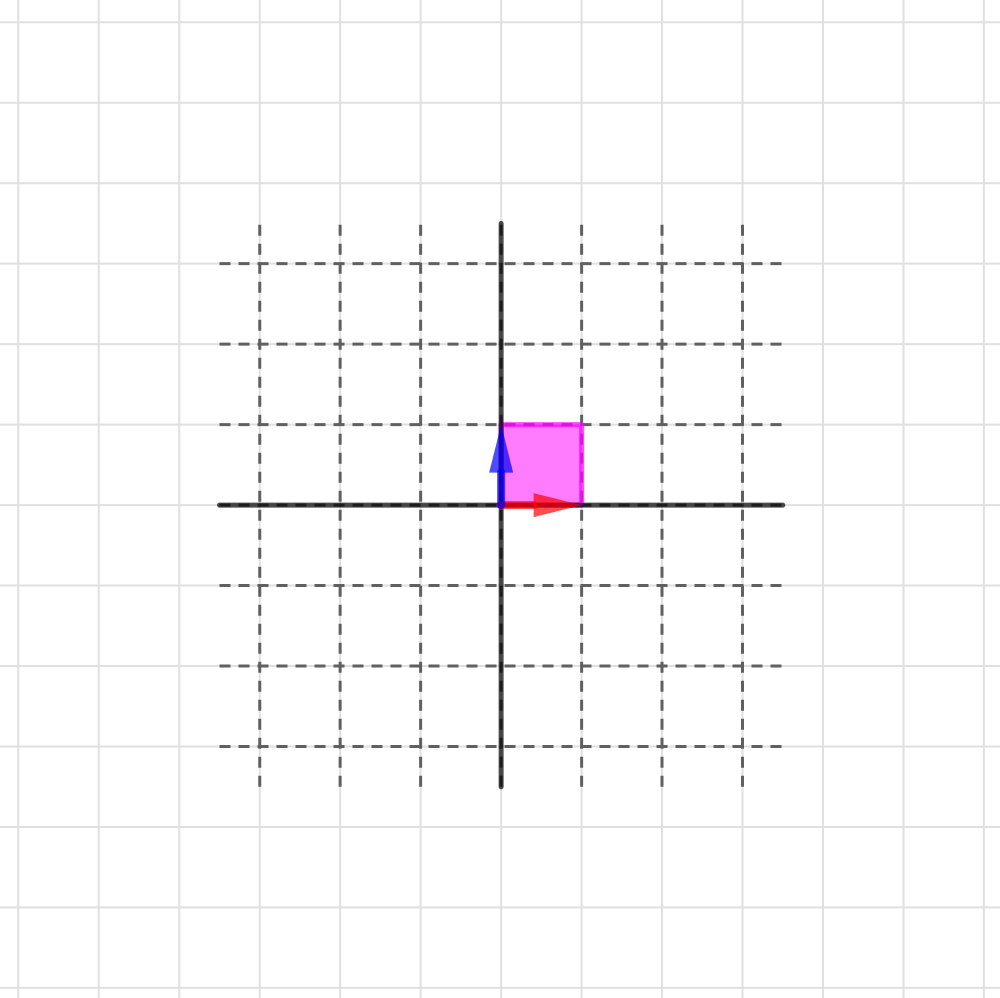
この正方形の乗っている座標を、例えばという行列で変換すると、その正方形は横に3、縦に2、引き伸ばされてその面積は6になります。
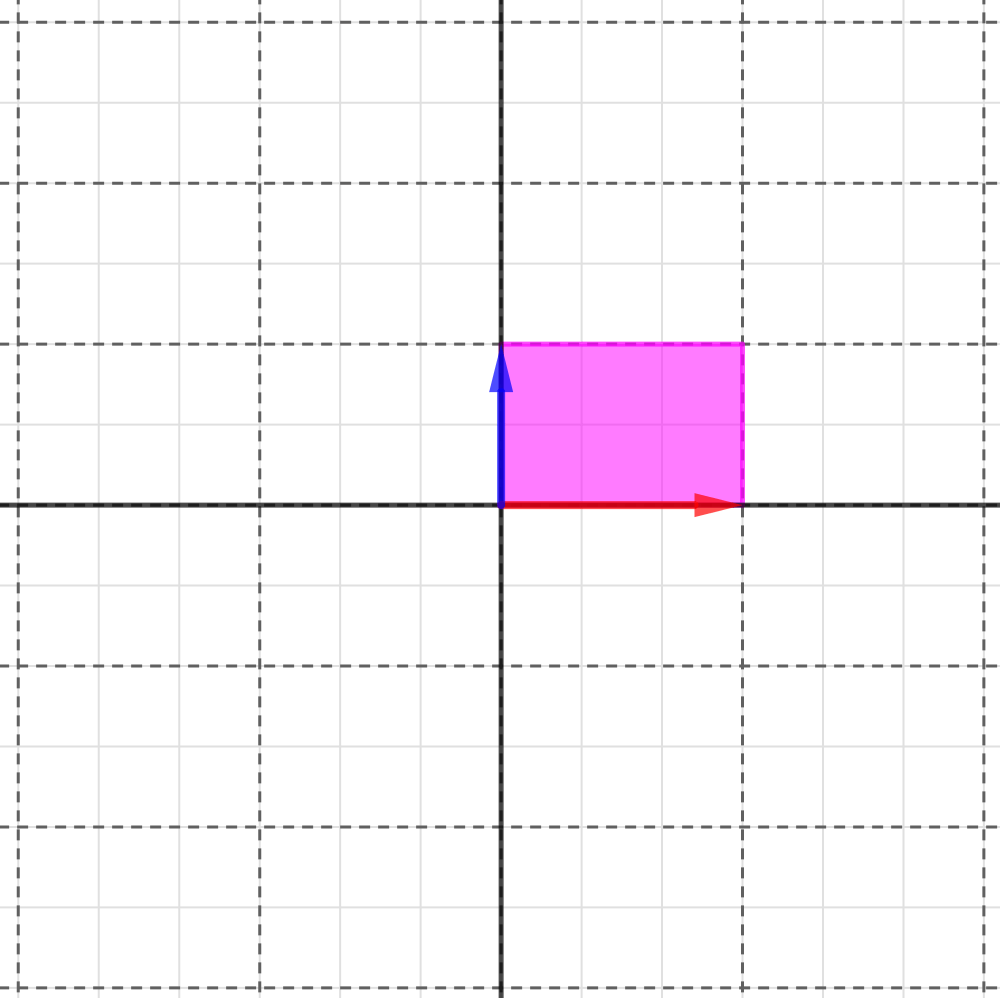
はい。この「6」という値こそが、という行列の行列式というわけだったんです。
「行列式」という名前をしているので、よく知らない人からすればそれって「式」なの?と思われがちなのですがこれは「値」です。それぞれの行列がもつ、固有の値です。
英語では行列式は「determinant(デターミナント)」といい、こっちのほうがまだ「なにか固有の値なんだよ感」が出ていると思います。
表記としてはや
などのように書かれます。
さて、ここで他の例として、という行列の行列式を考えてみます。
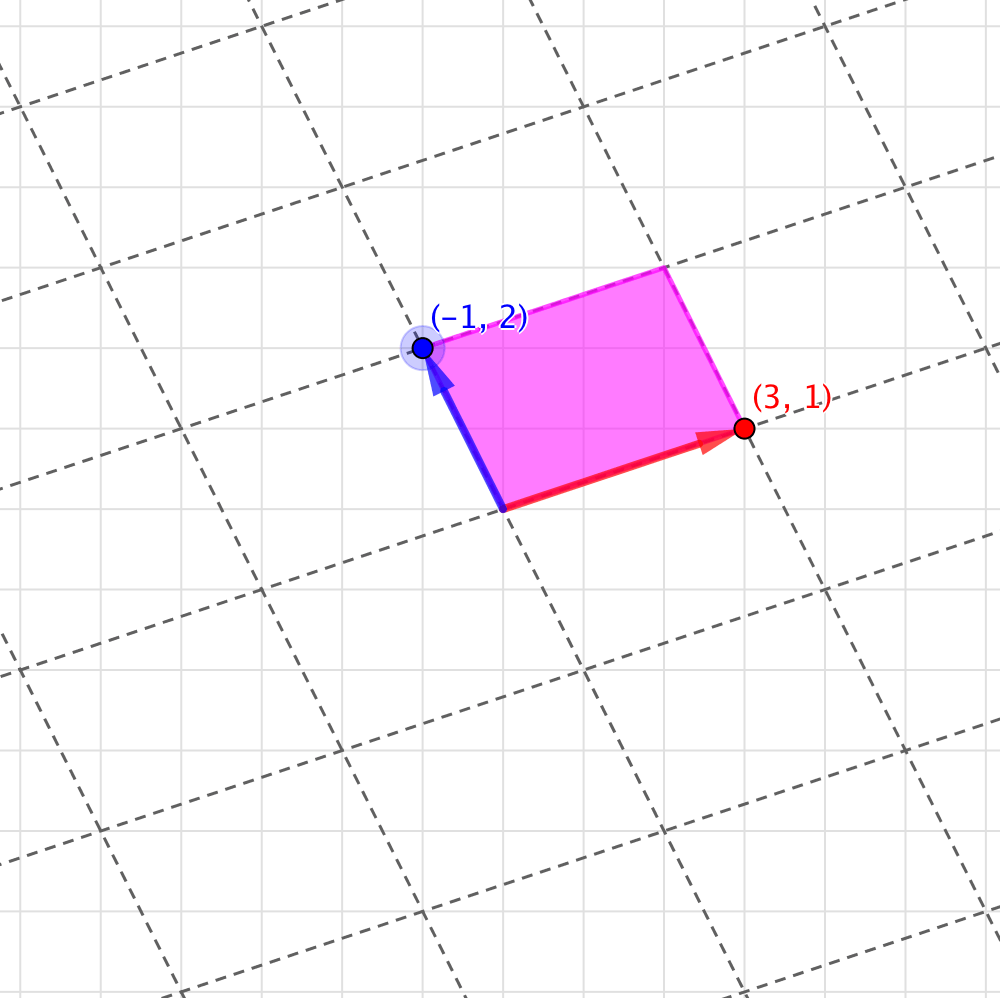
もとの正方形は平行四辺形になり、格子を数えればその面積は7であることがわかります。この「7」が、この行列の行列式というわけです。
……あまり面白くないですか? そうなんですよ。私も始めて行列式に触れたとき「平行四辺形の面積が行列式だよ」って聞いてもぜんぜんときめかなかったんですよね。あんなにみんな行列式行列式言って大事そうに扱ってるのにたったそんだけのこと?って。そんなの求めて何が嬉しいの?って。
私がときめいたのはこれです。
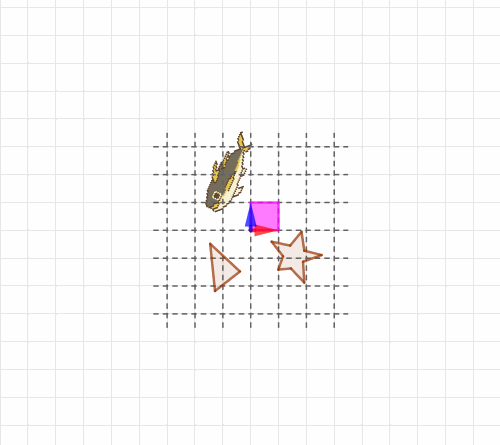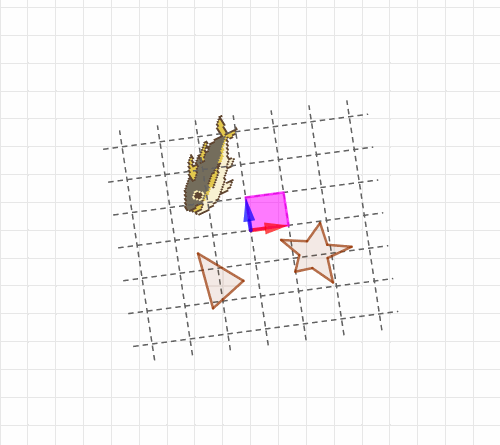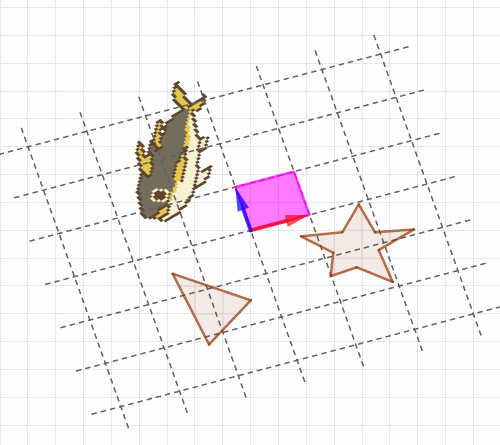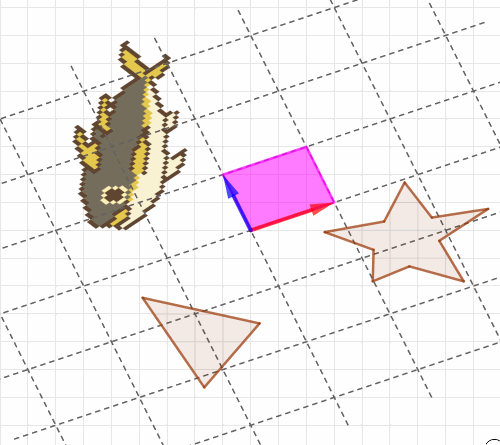
行列式とは、単に平行四辺形の面積というだけではなくて「座標全体がどれくらい伸び縮みするかの値」でした。つまりの1×1正方形だけじゃなくて、
くらいの場所にある三角形も7倍に、星型も7倍に、あるいはもっと複雑な形をした図形(鯵)も7倍になることがわかる!という、強力なツールだったわけです。多角形の一種である三角形や星型ならまだしも、いびつな形や複雑な形のものまで「7倍」ということがわかる。とてつもないありがたみです。私はこれでずいぶん世界がひらけた感じがしたものです。
それにしても、まさに「倍率」という言葉がぴったりですよね。すべて忘れてしまっても、「行列式は倍率」という言葉さえ覚えておけば、きっといつか思い出せます。
まとめ
ここまで、「行列式」とはどんなものなのかについて駆け足で見てきました。その大体の輪郭はつかめたのではないかと思います。まとめます。
・座標変換のうち、直線と原点を変えないものを線形変換という。
・線形変換は、基底ベクトルがそれぞれどう変化するかだけで記述できる。
・基底ベクトルがそれぞれどう変化するかは、一つの行列を使ってまとめて記述できる。
・ゆえに、行列とは線形変換であるといってよい。
・ある行列(≒線形変換)からは、「その変換によって座標全体がどれくらい伸び縮みするか」という値を取り出すことができる。
・その値こそが、行列式である。
こうまとめると簡単ですが、この記事は予備知識ゼロからを想定しているので、駆け足といいながらも結構長くなってしまいましたね。ここらでいったん切っておきましょう。
ごくごく簡単に言って、行列式とは「面積(体積、でもいいけど)」のことだと思っておいてください。捉えやすいというのもありますが、そうしておくことにより逆に面積とか全然関係ない行列式の利用法に出くわしたときに、えっ面積を表すだけだと思ってた行列式にそんな使い方が!?ってなってより感動することができるようになると思います。
さて、大体の輪郭は見えた行列式ですが、次の記事ではその具体的な計算と、行列式の値がマイナスや0など特別な値を取るときの振る舞いについて、少しだけ触れることにします。「マイナスの面積」とかいう概念が出てきてちょっと面白いです。
(11/13追記)書きました。 行列式が0だったりマイナスだったりするときの話 - アジマティクス
そしてさらにその先では、難しそうに思えるけどわかってみたら実はそんな大したことない概念「固有ベクトル」「固有値」を取り上げることを予定しています。
それでは今回はこのへんで! 次回お楽しみに!

高校数学でわかる線形代数―行列の基礎から固有値まで (ブルーバックス)
- 作者: 竹内淳
- 出版社/メーカー: 講談社
- 発売日: 2010/11/19
- メディア: 新書
- 購入: 4人 クリック: 31回
- この商品を含むブログ (6件) を見る

- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2018/10/17
- メディア: 単行本
- この商品を含むブログ (4件) を見る