2乗して-1になる数「」と、実数
を使って「
」と表される数を複素数といいます。
複素数は、和をとったり積をとったり逆数をとったりといろいろできるわけですが、それらを図示してみるときれいな構造が見えることがあります。
この記事は、細かい解説はそこそこにして、複素数を眺めてうわ〜きれいだね〜素敵だね〜っていう記事です。
複素平面
任意の複素数は、平面上の一点として表すことができます。
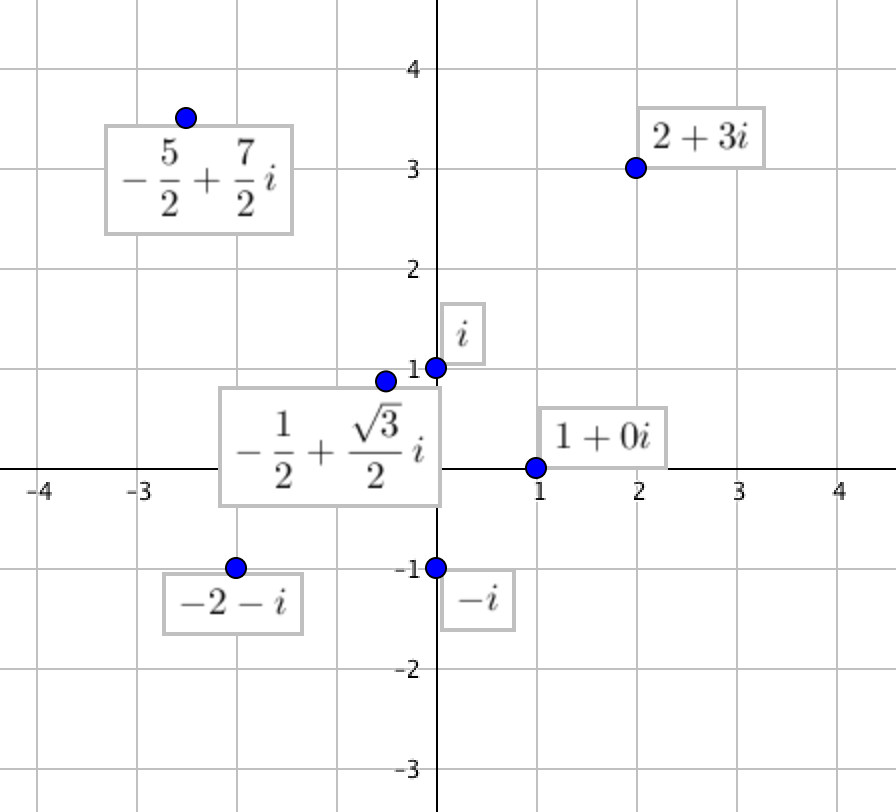
今でこそ「複素数といえば平面」というイメージがあるかもしれませんが、「複素数を平面上の一点として表す」というのは驚くほど画期的なアイデアです。
それまで、複素数は「方程式を解く途中にだけ出てきて、いざ解かれたあかつきには消えてしまう」という「便宜的な数」「虚構の数」と思われていました。
ガウスによって「複素平面」のアイデアが導入されてようやく複素数が図形的な表れを伴った。複素数にはそんな歴史があるようです。
今回の内容はすべて、そんな複素平面上で展開されるお話です。
複素数の和
2つの複素数の和は、実部どうし、虚部どうしの和で計算できます。これは図形的にはベクトルの和として見ることができます。

2つの数の和だったらハァそうですかって感じなんですが、複数の数でまとめてやってみると見えてくるものもあります。

青い点に赤い点を足した結果がピンクです。
はい。つまり複素数の足し算とは平行移動なわけですね。ベクトルの和の時点でそのことは現れていたわけですが、こうやって複数個の点で見てみるとよりそのことがはっきりします。
複素数の積
2つの複素数の積は、それぞれの軸からの角度(偏角)を足し、それぞれの原点からの距離(絶対値)をかけたもの、として計算できます。

こちらも複数の数でまとめてやってみると別の構造が見えてきます。
またしても青い点に赤い点の複素数をかけるわけですが、まずはかける数(赤い点)の偏角を0°に限定させてみます。つまり絶対値だけを変えてみるのです。

拡大・縮小変換になりました。かけた結果であるピンクの点の偏角は変わらずに、絶対値だけが変化していることになります。「偏角を足して、絶対値をかける」という複素数の積の計算規則から考えると当然といえば当然です。青に足されるはずの、赤の偏角が常に0なわけですからね。
また、赤い点がマイナスの時は鏡映変換にもなっていますね。
こんどは、赤い点の絶対値は1に保ったまま、偏角だけ変化させてみます。

回転ですね。かけた結果のすべての複素数(ピンク)の絶対値は変わらずに、偏角だけが変化していることになるからと考えれば当然です。かける数(赤)の絶対値が常に1なので。
偏角も絶対値も限定しない、自由な赤い点とかけてみると、

拡大・縮小と回転を組み合わせた変換になります。
「どこがどこに移動するか」の情報も入れてみましょう。

いいですねえ。
総合すると、も
も
も複素数であるような
は、拡大・縮小・鏡映・回転と平行移動を表せる、ということになります。
を赤、
を青で表示してみるとこんな感じ。

逆数
0以外の複素数は、逆数をとることができます。
いくつかの複素数を、その逆数の位置に移るように移動させてみました。

は? 魔界への扉じゃん
べき乗
「逆数をとる」というのは「乗する」と同じことです。ということでこんどは複素数
を「
乗」して、その
を1から-1まで連続的に変化させてみます。
「1乗」は何も変えないこと、「0乗」はすべての数を1にしてしまい、「-1乗」は逆数、ということからどんな動きになるか想像できるでしょうか。

赤い点がべき乗される点を表します。こっちはこっちで別のキモさがあります。
こんどは、2乗→3乗→4乗→…とどんどん増やしてみましょう。

みんなガヤガヤ動いてて楽しそうだなあって感じです。
世の中、点を少なくしたほうが逆に見えてくるものもあります。今のと同じ動きをの範囲の複素数にしぼって見てみましょう。

「どこがどこに」も表示します。

2つ以上の矢印の終点が一致していることがありますね。どういうときに一致するのか考えてみると何か見えてくるものがあると思います。
次は「乗」してみます。

謎のらせん構造みたいなのが見えてきてエモいです。
乗じられる赤い点を、単位円上にぐるぐる回してみましょう。1乗→乗→-1乗→
乗→1乗、と変化することになります。

こちらもこちらでいろいろ見えてくるものがあります。複素数においても1は何乗しても1のままなんだな、とか。
「どこがどこに」も表示。

もうだったらそんなケチくさいこと言わずに、赤い点を自由に動かします。

うひょー!
有名事実等
表示する点が多すぎて逆に見えなくなってるものもあるわけで、点の数をかなりしぼってみます。青い点に赤い点を乗じた結果がピンクなのは同じです。

「の
乗は実数」「
(オイラーの等式)」などの事実がご確認いただけるかと思います。
おわりに
いろいろな複素数の演算とそれらの「動き」を見てきました。数学の理論なんて一切わからなかったとしても、人は数学的対象を見て「キレイだなぁ〜」と思うことができます。当然、その感情は大事にするべきものです。その感情を抱いたという事実は、誰にも否定できるものではありません。
上記の画像たちを見て「キレイだなぁ〜」と思え、と言っているわけではありません。とくに何も思わなかったとしたら、それはそれで大事にするべき感情でしょう。
数学に対して「キレイだ」「美しい」「ロマンだ」と感動しているときに、もし「そんなものは数学ではない。数学の楽しみ方は他にももっとある」と言ってくる人がいたとしても、気にすることはありません。
あるものが数学であるか、そうでないかを決める権利は誰にもありません。「これは数学」「これは数学ではない」と弁別してしまうことは「選択と集中」の失敗に似ています。数学とは、どんなことから生まれるか分からないものであり、また、どんなことからも生まれうるものです。
たとえあるものが多くの人に「数学ではない」と認められたとしても、それが「数学への入り口」である可能性は否定できません。そして「数学に興味を持つきっかけは(「ロマン」や「美しい」などではなく)数学的対象でなくてはならない」といった共通認識は今のところありません。
「どんなことを入り口として数学に興味を持ったか」は人によって様々でしょうが、それを否定されたからといって引け目を感じる必要はありません。一般に、その思い出はその人にとって大切なものです。
また、「数学の楽しみ方は他にももっとある」はあまりにも当たり前ですので取り合う必要はありません。当たり前なのにそう言ってくる人がいたとしたら、その人は「この人は『ロマン』『美しい』以外の数学の楽しみ方を知らない」という前提を勝手においている可能性があります。取り合う必要はありません。
個人的な話ですが、私は数学においては「ロマン」や「美しい」に魅力を感じるほうではありません。どちらかといえば論理の話や構造の同一視などに魅力を感じます。それらをいろいろ深掘りした結果「美しい」が出てきたなら、それはそれでラッキーだなって思います。
さて、この記事は「うわ〜きれいだね〜素敵だね〜っていう記事」と冒頭で言いましたが、せっかくなので「他の楽しみ方」、つまりもう少し深入りできそうな話題を最後に置いておきましょう。
ある複素数と
について、
から始めて「
を2乗して
を足す」という操作を考えます。すなわち
→
という操作。
の範囲にあるいくつかの数を
として選んで、この操作を二回繰り返すとこうなります。

さらにここから三回、四回……というふうに続けていって、この操作を十数回繰り返して適用してみるとこうなります。

なんかやばいダルマみたいなのが出てきましたね。不規則にも見えるし、点の密度が高い部分を見ると規則的にも見えます。
十数回でこれということで、この回数をもっと増やす、さらに無限回繰り返すとどのような図形が出てくるのか気になるところです。
このことに興味があって、さらにネタバレも気にしない方は「マンデルブロ集合」などの言葉でググってみると今夜はよい夢が見られるでしょう。
さらにそこからどんどん興味の枝を伸ばしていっていただけると、私としては願ったり叶ったりでございます。
それでは今回はこのへんで!

