いままでのあらすじ
前回の記事(線形代数の知識ゼロから始めて行列式「だけ」理解する - アジマティクス)で、行列に対して定義される「行列式」というものをインストールしました。そこにいたるまでの道のりを振り返っておきます。前回の記事を読んでいない人はここさえ読んでおけば大丈夫です。
・座標変換のうち、直線と原点を変えないものを線形変換という。
・線形変換は、基底ベクトルがそれぞれどう変化するかだけで記述できる。
・基底ベクトルがそれぞれどう変化するかは、一つの行列を使ってまとめて記述できる。
・行列とは線形変換であるといってよい。
・行列(≒線形変換)からは、「その変換によって座標全体がどれくらい伸び縮みするか」という値を取り出すことができる。
・その値こそが、行列式である。
この記事では、そんな行列式にまつわるあれやこれやを拾っていきます。
行列式の計算
実際に行列が与えられたときにそこから行列式を計算するのは、一般には簡単ではありません。具体的に知りたければ「余因子展開」とか「サラスの方法」とかでよろしくおググりください。
ただし2×2行列に関しては「
」という式で簡単に求めることができます。なぜこの式になるかは、以下の図で納得することもできます。

この図はこれより高次元では表現できないので、まあ、ごまかしなんですが。
さて、では実際にこの式を、前の記事の最後の方に出てきた行列に当てはめて計算してみます。
、
、
、
ということです。前回の記事で言ったとおり、この行列の行列式は7でした。それは格子を数えても求められたわけですが、
で計算してみると確かにその値は
で
になっていることが確かめられます。
こんどは「左に90°回転」を表すで
を計算してみるとこれは1となり、確かにいくらグルグル回しても面積は変化しないのでそりゃ1だよねって感じです。
「回しても面積は変化しないことを行列式が表現できている」と捉えることもできるでしょう。
どういう意味があるのかはちょっとよくわからないんですが、ここで角度のときの一般の回転行列と、三角関数の代表的な公式を一つ置いておきますね。
一般の回転行列:
三角関数の公式:
いったいどういう意味があるんでしょうね。まったくわかりませんね。
符号付き面積
ここからはいろいろな行列について行列式を求めることで、行列式のいろいろな側面を眺めてみることにします。
という行列の行列式はどうなっているでしょうか。これを計算すると
。マイナスがでてきました。行列式って面積とか倍率とかの話だったはずなのにマイナスってどういうこと?
実はこの符号にも、意味を見出すことができるのです。がどういう線形変換を表すか見てみましょう。
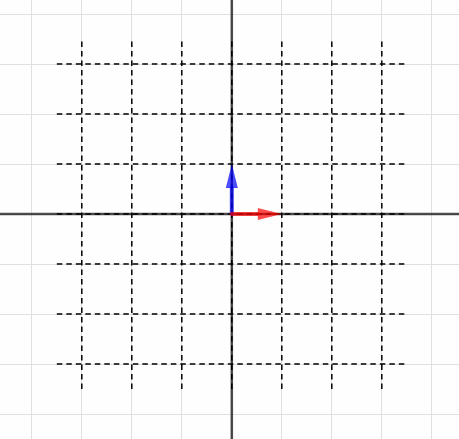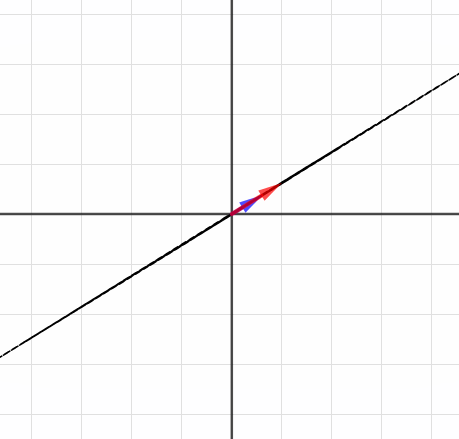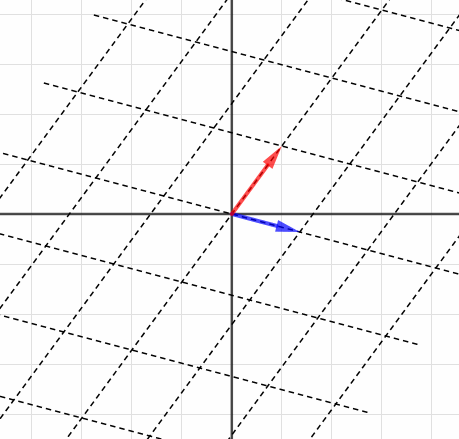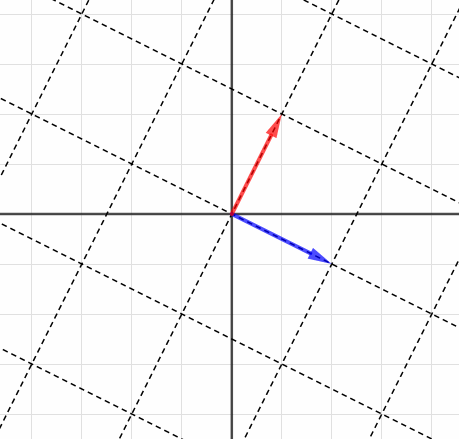
百聞は一見に如かずっていい言葉ですね。見たらすぐわかる。つまり、「裏返るとマイナス」なわけですね。もとの座標が折り紙の色のついた面だとすれば、マイナスは白色、裏面です。
ここで出てきた値は絶対値を取ると面積そのものとなり、つまり行列式はその値で「座標全体がどれだけ伸び縮みするか」に加えて、その符号で「座標が裏返っているかどうか」を表現しているといえます。
「マイナスの面積」ってなんか「裏世界の住人」っぽくて、封印されたはずの厨二心がざわめきます。マイナスの面積を持つ部屋に住んでみたりとかしたいですね。
行列の中で任意の2列を入れ替えると、必ず「裏返るかどうか」が変わることが知られています。これは2×2行列で言うなら、基底ベクトルのと
の「行き先」を入れ替えることと同じです。

「なにか変換を施すと符号だけ変わる」という性質は「反対称性」と呼ばれており、行列式では列の交換に対して反対称性が成り立っている、ということになります(もっと言うと、行の交換に対しても)。
逆行列の存在
ある線形変換について、それを「もとに戻す」線形変換を考えることができます。「2倍の拡大」だったら「1/2に縮小」。「左に90°回転」なら「右に90°回転」あるいは「左に270°回転」(同じことです)。「x軸に対する鏡映」だったら「x軸に対する鏡映」。つまり鏡映では同じことをもう一回やるともとに戻る、と。
「ある行列による線形変換に対して、さらに行列
で線形変換を施してやると、結果的には何も変えない」というとき、
を
に対する逆行列といいます。このとき、逆に
のほうも
に対する逆行列になります。
さて、ここでという行列について、
で行列式を計算してみます。すると0になりました。面積が0になるとはどういうことでしょうか? こういうことです。
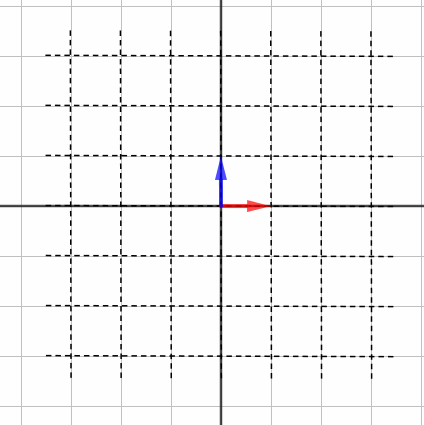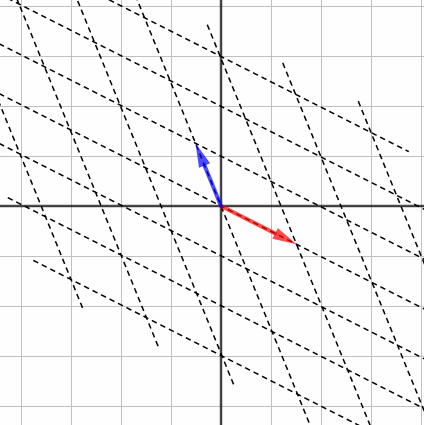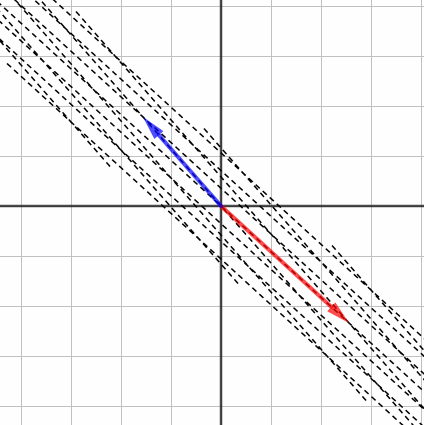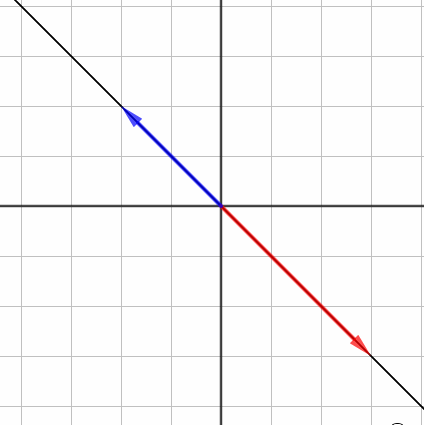
つまり、座標全体が「つぶれる」とき、行列式は0になるんですね。
ではこの「つぶれる」線形変換の逆行列はどうなっているかという話なのですが、実はこれ「逆行列は存在しない」のです。
なぜって、直線をどのように線形変換しても平面にはできない(元に戻せない)からといえます。あるいは、もとの座標平面がつぶれることによって、元に戻すのに必要な情報が失われてしまうから、ということもできるでしょう。すなわち、不可逆変換。不可逆変換に逆変換は存在しません。
「逆行列が存在しない」と「行列式が0」は同値です。なので、ある行列が与えられたときに、その行列式が0かどうか調べさえすれば、その行列に逆行列が存在するかどうかが分かるのです。便利。
逆行列の存在する行列、すなわち行列式が0でない行列のことを正則行列といいます。簡単に言えば、「つぶれない行列」ってことですね。ちなみに、ある次元の正則行列全体は群をなす(いい感じの構造をもつ)ことが知られています(一般線形群)。さらにその中でも行列式が「1」になる行列全体、つまり「つぶさず、倍率も変えない」行列全体も、こっちはこっちでいい感じの構造をもつことが知られています(特殊線形群)。
まとめ
ここまで、行列の倍率的要素である行列式についていろいろ見てきました。これらは、方程式が解けるかどうかの判定や、グラフの構造がどうなっているか見るのに使われたりして大事な概念なのですが、利用法が大事であることをさておいてもそれ自体とてもおもしろい概念だと思います。
ひとつ残念なことがあってですね、「行列式」やなんかでググるとかなり多くの割合でその「計算方法」が出てきます。もちろんそれはそれで大事なのですが、そればっかり出てくるのでみんなそんなに行列式を計算することしか興味ないのかな? なんて思ってしまいます。
もったいないと思うんですよね、それは本質的にこんなに面白い概念なのにテストをこなすための計算方法にばかり興味を持たれているなんて。学生時代に意味もよくわかっていないままにサインコサインの公式を覚えまくって、ただただ問題に当てはめていくだけのことをしていたのを思い出します。もったいないです。
行列式は数学のあらゆるところに登場するので親しくなっておいて損はない概念です。これを機に、計算法だけではない行列式の様々な側面を知っておくと、よりよい数学生活が送れると思います。では今回はこのへんで!